Wirkungsgrad und Leistung
Triebwerke und Motoren verrichten Arbeit, indem sie Dinge bewegen. Benzin- und Dieselmotoren geben die in ihrem Kraftstoff gespeicherte Energie ab. Elektromotoren geben Energie ab, die sie von einer Batterie oder einem Generator beziehen. Der menschliche Körper ist auch eine Form von Motor. Er gibt die in Lebensmitteln gespeicherte Energie ab.
Kraft, Arbeit und Energie
- Arbeit wird in Joule (J) gemessen.
- Energie wird in Joule (J) gemessen.
- Verrichtete Arbeit = umgewandelte Energie
- Kraft wird in Newton (N) gemessen.
- Arbeit = Kraft $\cdot$ Weg.
Wirkungsgrad
Ein Motor arbeitet nur mit einem Teil der ihm zugeführten Energie, der Rest wird als thermische Energie (Wärme) ungenutzt abgegeben. Der Wirkungsgrad eines Motors kann wie folgt berechnet werden:
$\mathrm {Wirkungsgrad \ = \ \frac{Nutzbare \ Arbeit}{Energie \ input}}$
oder
$\mathrm {Wirkungsgrad \ = \ \frac{Nutzbare \ Energie}{Energie \ input}}$
Wenn zum Beispiel ein Benzinmotor pro 100 J eingesetzte Energie 25 J Arbeit verrichtet, ist sein Wirkungsgrad $\smash {\frac{1}{4}}$ oder 25%. Mit anderen Worten, seine nutzbare Energie beträgt $\smash {\frac{1}{4}}$ des gesamten Energieeinsatzes.
| Energie-Einsatz | Arbeit | Wirkungs-grad | |||
|---|---|---|---|---|---|
| 100 J |
 |
 |
 |
25 J | 25 % |
| Benzinmotor | |||||
| 100 J |
 |
 |
 |
35 J | 35 % |
| Dieselmotor | |||||
| 100 J |
 |
 |
 |
80 J | 80 % |
| Elektromotor | |||||
| 100 J |
 |
 |
 |
15 J | 15 % |
| menschlicher Körper | |||||
Die obige Tabelle zeigt die Wirkungsgrade einiger typischer Motoren und Antriebe. Der geringe Wirkungsgrad von Motoren mit Kraftstoffverbrennung ist nicht auf eine schlechte Konstruktion zurückzuführen. Wenn ein Stoff verbrennt, ist es nicht möglich, seine gesamte thermische Energie in kinetische (Bewegungs-) Energie umzuwandeln, ohne dass ein Großteil davon ungenutzt bleibt.
Leistung
Ein kleiner Motor kann genauso viel Arbeit verrichten wie ein großer Motor, aber es dauert länger. Der große Motor kann schneller arbeiten. Die Geschwindigkeit, mit der Arbeit verrichtet wird, nennt man Leistung.
Typische Werte für Leistung
- Waschmaschine 250 W
- Sportler 400 W
- kleines Auto 35.000 W
- großes Auto 150.000 W
- Flugzeugturbine 75.000.000 W
1 kW = 1000 W
Die Pferdestärke (PS) ist eine Einheit der Leistung, die auf die Zeit der ersten Dampfmaschinen zurückgeht:
- 1 PS = 746 W (rund $\scriptsize \frac{3}{4}$ Kilowatt)
Die SI-Einheit der Leistung ist das Watt $(W)$. Eine Leistung von 1 Watt bedeutet, dass pro Sekunde 1 Joule Arbeit verrichtet wird (oder Energie umgewandelt wird). Die Leistung kann wie folgt berechnet werden:
$\mathrm {Leistung \ = \ \frac{verrichtete \ Arbeit}{benötigte \ Zeit}}$
oder
$\mathrm {Leistung \ = \ \frac{umgewandelte \ Energie}{benötigte \ Zeit}}$
Wenn ein Motor beispielsweise in 2 Sekunden 1000 Joule nutzbare Arbeit verrichtet, beträgt seine Leistung 500 Watt (500 Joule pro Sekunde).
Da Energie und Leistung in Beziehung stehen, gibt es eine weitere Möglichkeit, den Wirkungsgrad eines Motors zu berechnen:
$\mathrm {Leistung \ = \ \frac{Nutzleistung \ output}{Leistung \ input}}$
Probleme mit der Leistung
Beispiel 1
Das Auto hat eine konstante Geschwindigkeit von 30 $\smash{\mathrm{\frac{m}{s}}}$. Wenn die gesamte Reibungskraft des Fahrzeugs 700 N beträgt, welche Nutzleistung überträgt der Motor an die Antriebsräder?
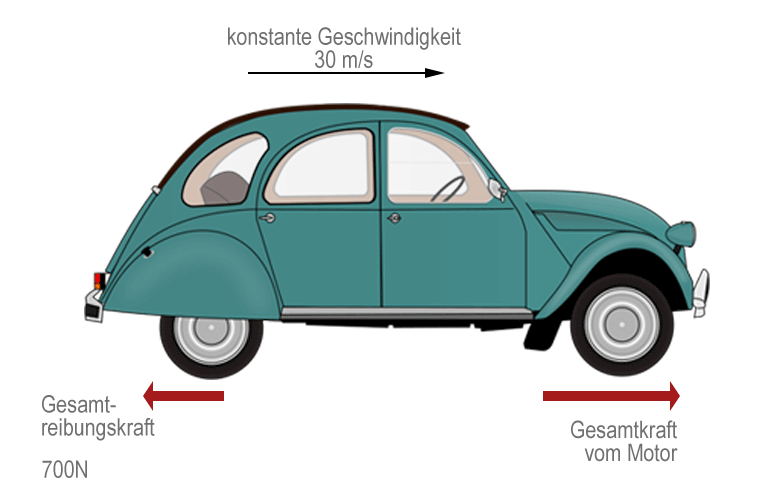
Da die Geschwindigkeit konstant ist, muss der Motor eine Vorwärtskraft von 700 N bereitstellen, um die gesamte Reibungskraft auszugleichen. In 1 Sekunde bewegt sich die 700 N Kraft um 30 m weiter, also:
verrichtete Arbeit = Kraft $\cdot$ Weg = 700 N $\cdot$ 30 m = 21.000 J.
Da der Motor in 1 Sekunde 21.000 J Nutzarbeit leistet, muss seine Nutzleistung 21.000 W oder 21 kW betragen.
Probleme dieser Art können auch mit dieser Gleichung gelöst werden:
$\mathrm {Leistung \ = \ Kraft \ \cdot \ Geschwindigkeit}$
Beispiel 2
Der Kran hebt in 20 s einen Betonblock von 100 kg in eine vertikale Höhe von 16 m. Wenn die Leistungsaufnahme des Motors 1000 W beträgt, wie hoch ist der Wirkungsgrad des Motors?
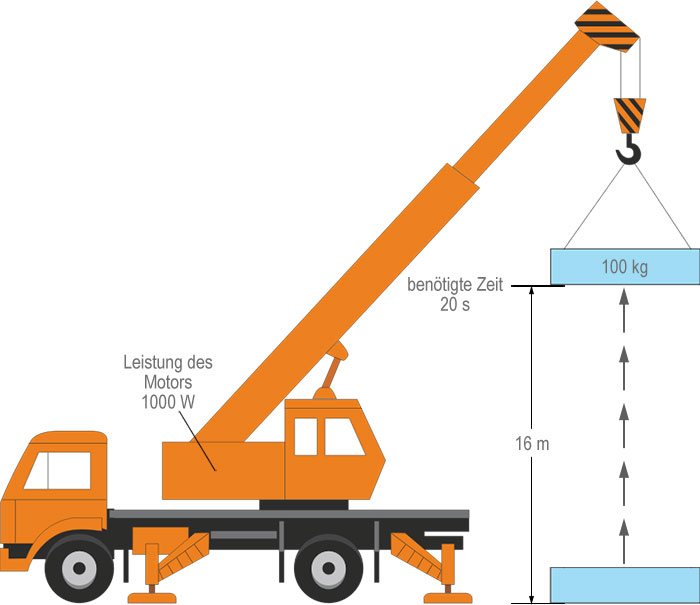
Auf der Erde ist $g \ = \ 10 \smash{\mathrm{\frac{N}{kg}}}$, also hat ein 100 kg Block ein Gewicht von 1000 N. Daher ist eine Kraft von 1000 N erforderlich, um den Block anzuheben. Wenn der Block angehoben wird:
$\mathrm {Arbeit \ = \ Kraft \ \cdot \ Weg \ = \ 1000N \ \cdot \ 16m \ = \ 16.000 \ J}$
$\mathrm {Leistung \ = \ \frac{Arbeit}{Zeit} \ = \ \frac{16.000 \ J}{20 \ s} \ = \ 800 \ W}$
$\mathrm {Wirkungsgrad \ = \ \frac{Nutzleistung}{zugeführte \ Leistung} \ = \ \frac{800\ W}{1000 \ W} \ = \ 0,8}$
Also hat der Motor einen Wirkungsgrad von 80%.
Fragen
1. Ein Motor leistet 1500 J Nutzarbeit, wobei 5000 J Energie zugeführt werden müssen.
- Wie hoch ist die Leistung des Motors?
- Was passiert mit dem Rest der Energie?
Richtig ist:
- 30 %
- Der Rest der Energie wird in nicht nutzbare Formen umgewandelt
Richtig ist:
500 W
3. Ein Motor hat eine Nutzleistung von 3 kW.
- Was ist seine Nutzleistung in Watt?
- Wie viel nutzbare Arbeit verrichter er in 1 s?
- Wie viel nutzbare Arbeit verrichter er in 20 s?
- Wenn die Leistungsaufnahme des Motors 4 kW beträgt, wie hoch ist der Wirkungsgrad?
Richtig ist:
- 3000 W
- 3000 J
- 60.000 J
- 75 %
4. Jemand zieht eine Last von 600 N mit einem Seil in 20 s auf eine vertikale Höhe von 10 m.
- Wieviel Arbeit verrichtet er?
- Wieviel Arbeit verrichtet er in 1 s?
- Was ist seine Nutzleistung?
Richtig ist:
- 6000 J
- 300 J
- 300 W
5. Ein Kran hebt eine Masse von 600 kg in 18 s in eine vertikale Höhe von 12 m.
- Welches Gewicht (in N) hebt der Kran?
- Was ist die Nutzleistung des Krans?
Richtig ist:
- 6000 N
- 4000 W
Richtig ist:
50.000 W