Zahlen und Einheiten
Physikalische Größe
Das Ergebnis einer Messung könnte, wie unten dargestellt, so aussehen:
$\mathrm {Zurückgelegter \ Weg = 10m}$
Das Ergebnis einer Messung nennt man physikalische Größe.
Eine physikalische Größe besteht aus zwei Teilen: einer Zahl und einer Einheit.
10 m bedeutet eigentlich $\mathrm {10 \ \dot \\ m}$ (10 mal Meter). In der Algebra bedeutet 10 $\mathrm {x}$ ebenfalls 10 $\mathrm {\dot \ x}$. Im obigen Fall kann man das Symbol für Meter (m) wie in einer Gleichung in der Algebra behandeln. Dieses Wissen ist wichtig, wenn man Einheiten kombinieren will.
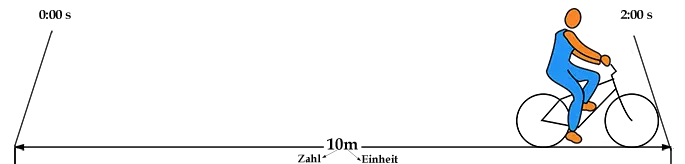
Kombinieren von Einheiten
In der Zeichnung oben legt der Fahrradfahrer 10 Meter in 2 Sekunden zurück. Er fährt also 5 Meter in jeder Sekunde. Die Geschwindigkeit beträgt also 5 Meter pro Sekunde. Um die Geschwindigkeit zu bestimmen, teilt man die zurückgelegte Distanz durch die Zeit, die man dafür benötigt:
$\mathrm {Geschwindigkeit = \frac{\Large 10m}{\Large 2s}}$ (s ist das Symbol für Sekunde)
Da man $\mathrm {m}$ und $\mathrm {s}$ wie Symbole in der Algebra behandeln kann, lautet die Gleichung:
$\mathrm {Geschwindigkeit = \frac{\Large 10}{\Large 2} \cdot \frac{\Large m}{\Large s} = 5 \frac{\Large m}{\Large s}}$
Um Platz zu sparen, schreibt man für gewöhnlich $\mathrm {5 \ m/s}$.
Folglich ist $\mathrm {m/s}$ die Einheit für Geschwindigkeit.
Richtig und falsch
Diese Gleichung ist korrekt: $\mathrm {\frac{\Large 10m}{\Large 2s} = 5 m/s}$.
Diese Gleichung ist falsch: $\mathrm { \ \frac{\Large 10}{\Large 2} \ \ = 5 m/s}$.
Sie ist deshalb falsch, weil die Symbole $\mathrm {m}$ und $\mathrm {s}$ weggelassen wurden. 10 geteilt durch 2 ist 5 und nicht 5 m/s.
Genaugenommen müssen die Einheiten bei jedem Rechenschritt angegeben werden, nicht nur bei der Lösung.
Größer und kleiner
Um eine Einheit zu vergrößern oder zu verkleinern, kann man Extrasymbole davor setzen. Solche Symbole nennt man Präfix.
| Präfix | Bedeutung | Beispiel | |
|---|---|---|---|
| G (giga) | 1.000.000.000 | (109) | GB (Gigabyte) |
| M (mega) | 1.000.000 | (106) | MW (Megawatt) |
| k (kilo) | 1.000 | (103) | km (Kilometer) |
| d (dezi) | $\mathrm {\frac {1}{10}}$ | (10-1) | km (Kilometer) |
| c (centi) | $\mathrm {\frac {1}{100}}$ | (10-2) | cm (Zentimeter) |
| m (milli) | $\mathrm {\frac {1}{1.000}}$ | (10-3) | mm (Millimeter) |
| µ (micro) | $\mathrm {\frac {1}{1.000.000}}$ | (10-6) | µm (Micrometer) |
| n (nano) | $\mathrm {\frac {1}{1.000.000.000}}$ | (10-9) | nm (Nanometer) |
| $\mathrm {1000 \ \ = \ 10 \cdot \ 10 \cdot \ 10 = 10^3}$ |
| $\mathrm {100 \ \ \ \ = \ 10 \cdot \ 10 \qquad = 10^2}$ |
| $\mathrm {0,1 \ \ \ \ = \ \frac{1}{10} \qquad \qquad = 10^{-1}}$ |
| $\mathrm {0,01 \ \ = \frac{1}{100} \ = \ \frac{1}{10^2} \;\;\; = 10^{-2}}$ |
| $\mathrm {0,001 \ = \frac{1}{1000} \ = \ \frac{1}{10^3} \ = 10^{-3}}$ |
Wissenschaftliche Notation
Die wissenschaftliche Notation ist eine Form der modernen Zahlendarstellung. Hier ein Beispiel: in einem Fremdenführer steht, dass die Einwohnerzahl von Frankfurt am Main ca.
$\mathrm 730.000$
beträgt.
Mit der Darstellung dieser Zahl in dieser Form gibt es zwei Probleme:
- Das Schreiben von vielen Nullen ist recht unbequem und
- meistens sind sie nur dazu da, um zu zeigen, dass es sich um eine sechsstellige Zahl handelt.
Dieses Problem kann man vermeiden, wenn man die Zahl als 10er - Potenz darstellt:
$\mathrm {7,3 \cdot 10^5 \qquad \qquad (10^5 \ = \ 10 \cdot \ 10 \cdot \ 10 \cdot \ 10 \cdot \ 10 \ = \ 100000)}$
| Dezimal | Bruch | Wissensch. Notation |
|---|---|---|
| $\mathrm {500}$ | $\mathrm {5 \cdot 10^2}$ | |
| $\mathrm {0,5}$ | $\mathrm {\frac{5}{10}}$ | $\mathrm {5 \cdot 10^{-1}}$ |
| $\mathrm {0,05}$ | $\mathrm {\frac{5}{100}}$ | $\mathrm {5 \cdot 10^{-2}}$ |
| $\mathrm {0,005}$ | $\mathrm {\frac{5}{1000}}$ | $\mathrm {5 \cdot 10^{-3}}$ |
$\mathrm {7,3 \cdot 10^5}$ sagt aus, dass die Zahlen 7 und 3 wichtig sind. Die Zahl hat also zwei bedeutende (signifikante) Stellen. Wenn die Einwohnerzahl der Stadt genauer angegeben wäre, beispielsweise auf drei signifikante Stellen genau, kann man sie so aufschreiben:
$\mathrm {7,32 \cdot 10^5}$
Zahlen in Zehnerpotenzen sind in der wissenschaftlichen Notation dargestellt. Die Beispiele rechts haben eine signifikante Stelle, nämlich die Zahl 5.
Fragen
Hinweis: Antworten können aufgeklappt werden
Richtig ist:
3m x 2m = 6m2
Richtig ist:
| 2 km | 0,2 km | 20 km |
Richtig ist:
| 5 s | 50 s |
| 1.500 m | 1.500.000 m | 0,15 m | 0,015 m |
Richtig ist:
| 1,5 x 103 m | 1,5 x 106 m | 1,5 x 10-1 m | 1,5 x 10-2 m |