Impuls (1)

Man sagt, dass ein schweres Fahrzeug, das schnell fährt, viel Schwung hat. Allerdings nennt man diese physikalische Größe in der Physik "Impuls", und der ist exakt definiert:
$\mathsf {Impuls \ = \ Masse \ \cdot \ Geschwindigkeit}$
Wenn ein Modellauto beispielsweise eine Masse von
$\mathrm {2 \ kg}$
und eine Geschwindigkeit von
3 $\mathrm {\tfrac {m}{s}}$
hat, ist sein Impuls:
$\mathrm {2 \ kg \ \cdot \ 3 \ \frac {m}{s} \ = \ 6 \ \frac {kg \ \cdot \ m}{s}}$
Wie die Geschwindigkeit ist der Impuls ist ein Vektor, so dass oft ein + (Plus) oder ein - (Minus) verwendet wird, um seine Richtung anzuzeigen: Beispielsweise:
Impuls des Fahrzeugs nach rechts:
$\mathrm {+6 \ \frac {kg \ \cdot \ m}{s}}$
Impuls des Fahrzeugs nach links:
$\mathrm {-6 \ \frac {kg \ \cdot \ m}{s}}$
Die Beziehung zwischen Kraft und Impuls: Newtons zweites Gesetz der Bewegung
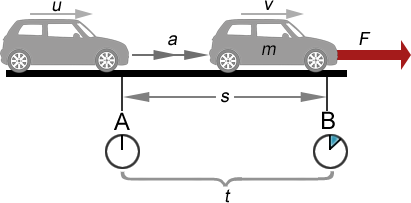
Eine Kraft wirkt auf ein Objekt mit der Masse m über die Zeit t. Als Folge erhöht sich seine Geschwindigkeit von u auf v, seine Beschleunigung über diese Zeit ist a.
Entsprechend dem zweiten newtonschen Gesetzt gilt:
$\mathsf {Kraft} \ = \ \frac {\mathsf {Impulsänderung}}{\mathsf {Zeit}}$
Mit Symbolen:
$F \ = \ \frac {mv - mu}{t} \ = \ \mathrm {m} (\frac {v - u}{t})$
Aber:
$a \ = \ (\frac {v - u}{t})$
Also:
$F \ = \ ma$
Wenn eine Kraft auf ein Objekt wirkt, wird es beschleunigt. Deshalb wird sich seine Geschwindigkeit ändern, ebenso sein Impuls. Die Kraft und die Änderung des Impulses werden durch diese Gleichung beschrieben:
$\mathsf {Kraft \ = \ \frac{Impulsänderung}{Zeit}}$
oder:
$\mathsf {\small {Kraft \ = \ Änderungsrate \ des \ Impulses}}$
Die Beziehung zwischen einer Kraft und der Änderungsrate des Impulses, die diese Kraft erzeugt, ist bekannt als Zweites newtonsches Gesetz der Bewegung.
Die obige Gleichung ist tatsächlich nur eine andere Art auszudrücken, dass $\mathrm {Kraft \ = \ Masse \ \cdot \ Beschleunigung}$. Der Kasten auf der linken Seite erklärt, warum.
Impuls
Stellt man die vorherige Gleichung um, dann folgt daraus:
$\mathsf {Kraft \ \cdot \ Zeit \ = \ Änderung \ des \ Impulses}$
Die Größe $\mathrm {Kraft \ \cdot \ Zeit}$ heißt Impuls.
Newton stellte fest, wenn dieselbe Kraft über die gleiche Zeit auf zwei unterschiedliche Massen wirkt, dann hat die größere Masse eine geringere Geschwindigkeit als die kleinere Masse, aber die Veränderung von "Masse $\cdot$ Geschwindigkeit" wäre in jedem Fall dieselbe. Es war diese Beobachtung, die zum Begriff Impuls und zu seinem zweiten Gesetz führte.
Aufgaben lösen
Beispiel 1
Ein Modellauto mit der Masse 2 kg fährt geradeaus. Wenn sich seine Geschwindigkeit von 4 $\mathrm {\frac {m}{s}}$ auf 9 $\mathrm {\frac {m}{s}}$ in 4 s erhöht, wie groß ist die Kraft, die darauf wirkt?
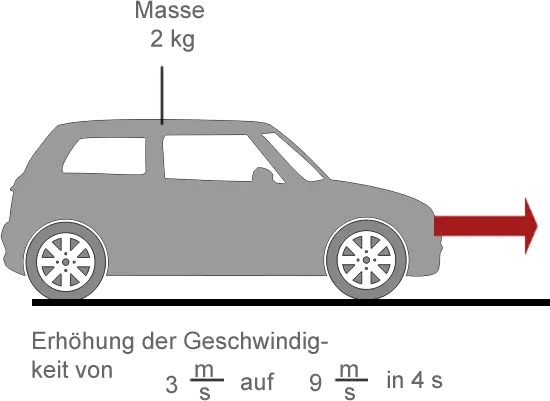
Wir beginnen mit:
$\mathsf {Impuls = Masse \cdot Geschwindigkeit} \ = \mathrm {2 \ kg \ \cdot \ 3 \ \frac {m}{s} \ = \ 6 \ \frac {kg m}{s}}$
4 Sekunden später:
$ \mathsf {Impuls = Masse \cdot Geschwindigkeit} \ = \mathrm {2 \ kg \ \cdot \ 9 \ \frac {m}{s} \ = \ 18 \ \frac {kg m}{s}}$
Also:
$\mathsf {Änderung \ des \ Impulses} \ = \ \mathrm {12 \ \frac {kg m}{s}}$
Aber:
$\mathsf {Kraft = \frac {Änderung \ des \ Impulses}{Zeit}} \ = \ \mathrm{\frac {12 \ kgm}{4 \ s}}$
Also:
$\mathsf {Kraft = 3 N}$
Das Problem kann auch gelöst werden, indem man die Beschleunigung des Fahrzeugs ausarbeitet und dann diese Gleichung verwendet:
$\mathsf {Kraft = Masse \cdot Beschleunigung}$
Beispiel 2
Eine kleine Rakete stößt jede Sekunde 2 kg Abgas mit einer Geschwindigkeit von 100 $\mathrm {\frac {m}{s}}$ aus. Welcher Schub (Kraft) wird vom vom Raketenantrieb erzeugt?

Durch das dritte newtonsche Gesetz der Bewegung ist die Schubkraft auf die Rakete gleich der Kraft, die auf das Abgas drückt. Diese Kraft kann berechnet werden, indem man die Rate der Impulsänderung des Gases herausfindet:
2 kg ausgestoßenes Gas legen in 1 Sekunde 100 $\mathrm {\frac {m}{s}}$ an Geschwindigkeit zu.
Also:
$\mathsf {Schub \ = \ \frac {Änderung \ des \ Impulses}{Zeit}} = \ \mathrm {\frac {200 \ kg \ {\frac {m}{s}}}{1 \ s}}$
Also:
$\mathsf {Schub \ = \ 200 \ N}$
Fragen
Antworten können aufgeklappt werden
Richtig ist:
Impuls = Masse $\cdot$ Geschwindigkeit
Richtig ist:
Impulsänderung = Kraft $\cdot$ Zeit

a) Wie groß der Impuls des Modellautos, bevor die Kraft wirkt?
b) Wie groß ist der Impuls, nachdem die Kraft gewirkt hat?
c) Wie groß ist die Impulsänderung?
d) Wie groß ist die Impulsänderung pro Sekunde?
e) Wie groß ist die resultierende Kraft auf das Modellauto?
Berechne diese Kraft in mehreren Schritten:
f) Wie groß ist die Geschwindigkeit des Modellautos?
g) Wie groß ist die Beschleunigung des Modellautos?
h) Welche Gleichung verbindet Kraft, Masse und Beschleunigung?
i) Wie groß ist die resultierende Kraft auf das Modellauto?
Richtig ist:
a) 48 $\mathrm {\tfrac {kgm}{s}}$
b) 72 $\mathrm {\tfrac {kgm}{s}}$
c) 24 $\mathrm {\tfrac {kgm}{s}}$
d) 8 $\mathrm {\tfrac {kgm}{s^2}}$
e) 8 N
f) 2 $\mathrm {\tfrac {m}{s}}$
g) 0,67 $\mathrm {\tfrac {m}{s^2}}$
h) Kraft = Masse $\cdot$ Beschleunigung
i) 8 N
a) Welchen Schub (Kraft) erzeugt die Turbine?
b) Wenn die Turbine die doppelte Masse des Gases bei der halben Geschwindigkeit ausstoßen würde, was wäre dann der Schub?
Richtig ist:
a) 7500 N
b) 7500 N