Bestimmung von Dichte und Volumen

Volumenbestimmung
Flüssigkeit
Ein Volumen von etwa einem Liter kann mit einem Messzylinder bestimmt werden. Wenn die Flüssigkeit in den Zylinder gegossen wird, zeigt die Höhe des Wasserspiegels auf der Skala das Volumen an.
Die meisten Messzylinder haben Skalen, die in Milliliter (ml) oder Kubikzentimeter (cm3) eingeteilt sind.
Regelmäßige Festkörper
Wenn ein Objekt eine einfache Form hat, kann sein Volumen ganz einfach berechnet werden. Beispielsweise:
$\mathrm {Volumen \ eines \ rechteckigen \ Blocks \ = \ Länge \ \cdot \ Breite \ \cdot \ Höhe}$
$\mathrm {Volumen \ eines \ Zylinders \ = \ Radius^{2} \ \cdot \ \pi \ \cdot \ Höhe}$
Unregelmäßige Festkörper
Wenn die Form eines Festkörpers zu ungünstig ist, um das Volumen zu berechnen, kann er in einen teilweise mit Wasser gefüllten Messzylinder abgesenkt werden, wie unten gezeigt. Der Anstieg des Pegels auf der Volumenskala ergibt sein Volumen. Angenommen der Festkörper schwimmt, dann kann man daran ein Metallstück befestigen, das ihn unter Wasser zieht. Dann wird das Gesamtvolumen bestimmt. Das Volumen des Metalls wird in einem separaten Experiment gemessen und dann von dem Volumen des ersten Experiments subtrahiert.

Dichtebestimmung
Die Dichte eines Materials kann man berechnen, sobald die Masse und das Volumen bestimmt wurden. Die Masse eines kleinen Festkörpers oder einer Flüssigkeit kann mit einer Waage bestimmt werden. Im Falle einer Flüssigkeit muß man daran denken, die Masse des Behälters zu berücksichtigen. Das Volumen kann dann wie oben beschrieben berechnet werden.
Archimedes und die Krone
Archimedes, ein griechischer Mathematiker, lebte um 250 v. Chr. in Syrakus in Sizilien. Er machte wichtige Entdeckungen über Hebel und Flüssigkeiten, ist aber wohl am bekanntesten wegen seiner klugen Lösung eines Problems, mit dem ihn der König von Syrakus beauftragt hatte.

Der König hatte seinem Goldschmied etwas Gold gegeben, um eine Krone daraus zu gießen. Aber als die Krone ausgeliefert wurde, war der König misstrauisch. Vielleicht hatte der Goldschmied etwas von dem Gold gestohlen und stattdessen billigeres Silber hinzugemischt.
Der König bat Archimedes, die Krone zu untersuchen. Archimedes wusste, dass die Krone die selbe Masse hatte, wie eine Krone aus purem Gold. Er wusste auch, dass Silber eine geringere Dichte als Gold hat. Also müsste eine Krone mit beigemischtem Silber ein größeres Volumen haben, als eine Krone aus purem Gold.
Aber wie könnte er das Volumen messen? Als er in seine Badewanne stieg - so erzählt die Legende - bemerkte Archimedes den Anstieg des Wasserspiegels. Das war die Antwort! Er war so aufgeregt, dass er aus seinem Bad sprang, nackt durch die Straßen rannte und "Eureka!" rief, was soviel bedeutet wie: "Ich habe es gefunden!"
Später setzte Archimedes die Krone in einen Wasserbehälter und maß den Anstieg des Wasserspiegels. Dann tat er das gleiche mit einer gleichen Masse von reinem Gold. Der Anstieg des Wasserspiegels war anders. Also konnte die Krone nicht aus reinem Gold bestanden haben.
Relative Dichte
Die relative Dichte eines Stoffes sagt dir, in welchem Verhältnis seine Dichte zu der eines anderen Stoffes steht. Beispielsweise kann man die Dichte eines Stoffes mit der Dichte des Wassers vergleichen. So wird die relative Dichte berechnet:
$\mathrm {relative \ Dichte \ = \ \frac {Dichte \ des \ Stoffes}{Dichte \ von \ Wasser}}$
Zum Beispiel hat Blei eine Dichte von 11.300 kg/m3 (11,3 g/cm3) und Wasser hat eine Dichte von 1000 kg/m3 (1 g/cm3). Damit:
$\mathrm {relative \ Dichte \ von \ Blei \ = \ \frac {11.300 \ kg/m^{3}} {1000 \ kg/m^{3}} \ = \ \frac {11,3 \ g/cm^{3}} {1 \ g/cm^{3}} \ = \ 11,3}$
Die relative Dichte hat keine Einheit. Sie ist eine Zahl, um Stoffe miteinander zu vergleichen. Die relative Dichte wurde früher als "spezifisches Gewicht" bezeichnet.
Dichte von Planeten
Die Dichte eines Planeten nimmt in Richtung des Kerns immer weiter zu. Trotzdem kann eine durchschnittliche Dichte bestimmt werden, indem die Gesamtmasse durch das Gesamtvolumen dividiert wird. Die Masse eines Planeten beeinflusst seine Anziehungskraft (Gravitation) und damit die Umlaufbahn eines jeden Mondes, der ihn umkreist. Wissenschaftler können die Masse eines Planeten daraus berechnen. Sein Volumen kann berechnet werden, sobald der Durchmesser bekannt ist.
Die durchschnittliche Dichte eines Planeten gibt Hinweise auf seine Struktur:
 |
|
Erde |
Jupiter |
| durchschnittliche Dichte: 5520 kg/m3 | durchschnittliche Dichte: 1330 kg/m3 |
|
Die durchschnittliche Dichte der Erde ist etwa doppelt so hoch wie das Gestein an ihrer Oberfläche. Das bedeutet, dass die Erde einen sehr dichten Kern haben muß - wahrscheinlich besteht er hauptsächlich aus Eisen |
Die niedrige durchschnittliche Dichte des Jupiter ist ein Grund, warum die Wissenschaftler glauben, dass Jupiter hauptsächlich aus Wasserstoff- und Heliumgas besteht und nur einen kleinen Kern aus Gestein besitzt. |
Fragen
Antworten können aufgeklappt werden
1. Nimm die Tabelle zu Hilfe und entscheide welche Krone aus Gold ist, welche aus Silber ist und welche aus einer Mischung besteht:
 Krone A |
 Krone B |
 Krone C |
|
| Masse (g) | 3750 | 3750 | 3750 |
| Volumen (cm3) | 357 | 194 | 315 |
| Dichte von Gold 19,3 g/cm3 | Dichte von Silber 10,5 g/cm3 | ||
Krone A: Silber, Krone B: Gold, Krone C: Mischung
2. Bestimme
a) Masse, Volumen und Dichte der Flüssigkeit (in g/cm3)
b) Masse, Volumen und Dichte des Steins (in kg/m3)
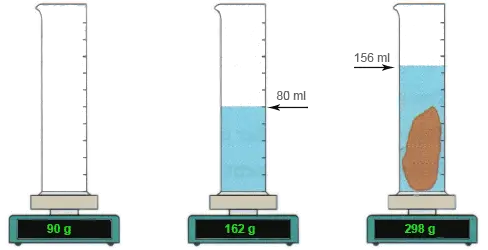
a) 72 g, 80 ml und 0,9 g/cm3
b) 136 g, 76 ml und 1789 kg/m3