Impuls (2)
Geschwindigkeit und Impuls
Geschwindigkeit und Impuls sind Vektoren. Beide haben sowohl eine Richtung als auch einen Betrag.
$\mathsf {\small{Impuls = Masse \cdot Geschwindigkeit}}$
$\mathrm {\frac {kgm}{s} = kg \cdot \frac {m}{s}}$
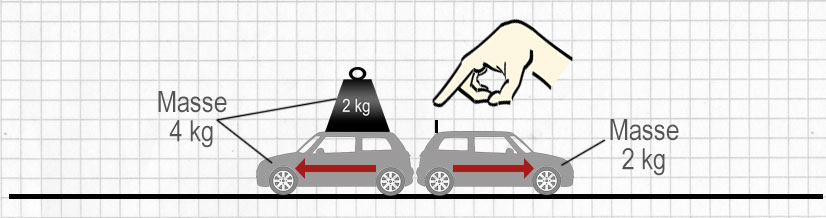
Zuerst bewegen sich die Modellautos unten nicht. Aber wenn ein mit einer Feder gespannter Kolben an einem Auto losgelassen wird, schießen sie in entgegengesetzte Richtungen auseinander. Ihre Geschwindigkeiten können mit Ticker-Tape-Timern gemessen werden.
| Bevor die Feder entspannt wird: | |
 |
|
| $\mathrm {Impuls = 0}$ | $\mathrm {Impuls = 0}$ |
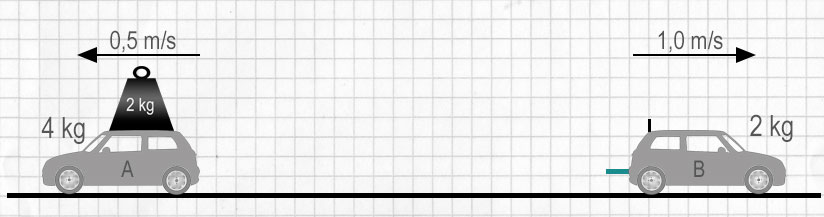
| Nachdem die Feder entspannt wurde: | |
 |
|
| $\mathrm {Impuls = 4kg \cdot 0,5 \frac {m}{s} = 2 kg \frac {m}{s}}$ | $\mathrm {Impuls = 2kg \cdot 1,0 \frac {m}{s} = 2 kg \frac {m}{s}}$ |
Wenn die Modellautos auseinander schießen, hat der Wagen mit der geringsten Masse die höchste Geschwindigkeit. Das Diagramm zeigt typische Masse- und Geschwindigkeitswerte. Diese veranschaulichen eine Regel, die für diese Experimente gilt:
$\mathsf {\small{Masse \ \cdot \ Geschwindigkeit \ nach \ links \ = \ Masse \ \cdot \ Geschwindigkeit \ nach \ rechts}}$
Dieses Ergebnis ist zu erwarten. Nach dem dritten newtonschen Gesetz der Bewegung sind die Kräfte, die auf die beiden Wagen wirken, gleich groß, aber in entgegengesetzter Richtung. Ebenso wirken die beiden Kräfte gleichzeitig. Somit sollten sie gleiche, aber entgegengesetzte Impulsänderungen verursachen, weil:
$\mathrm {Kraft \cdot Zeit = Impulsänderung}$
Impulserhaltung
Mit den oben genannten Masse- und Geschwindigkeitswerten kann der Gesamtimpuls der Wagen vor dem Versuch und danach ermittelt werden. Da ein Impuls ist ein Vektor ist, muß eine Richtung zulässig sein. In den folgenden Berechnungen wird ein Impulszuwachs nach rechts als positiv (+) gezählt:
Bevor die Feder entspannt wird:
Gesamtimpuls der beiden Wagen = $0$
Nachdem die Feder entspannt wurde:
Impuls des Wagens A =
$\mathrm {Masse \cdot Geschwindigkeit = 4 kg \cdot -0,5 \frac {m}{s} = -2 \frac {kg m}{s}}$
Impuls des Wagens B =
$\mathrm {Masse \cdot Geschwindigkeit = 2 kg \cdot 1,0 \frac {m}{s} = +2 \frac {kg m}{s}}$
Also auch hier:
Gesamtimpuls der beiden Wagen = $0$
So ist der Gesamtimpuls nach dem entspannen der Feder unverändert. Dies ist ein Beispiel für das Gesetz der Impulserhaltung:
Wenn zwei oder mehr Objekte aufeinander wirken, bleibt ihr Gesamtimpuls konstant, sofern keine anderen äußeren Kräfte wirken.
Problem der Kollision
| Vor dem Zusammenstoß: |
 |
| Nach dem Zusammenstoß: |
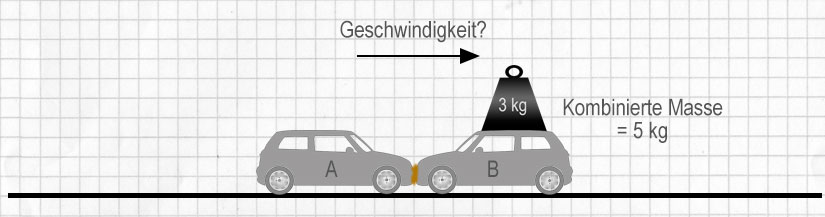 |
Beispiel
Die beiden Modellautos oben fahren aufeinander zu und stoßen zusammen, bleiben aber durch das Klebematerial aneinander haften. Wie hoch ist ihre Geschwindigkeit nach dem Zusammenstoß und in welche Richtung bewegen sie sich?
Nach dem Gesetz der Erhaltung des Impulses muß der Gesamtimpuls beider Wagen nach der Kollision gleich dem Gesamtimpuls vor der Kollision sein.
Kurz vor dem Zusammenstoß:
Impuls des Wagens A =
$\mathrm {Masse \cdot Geschwindigkeit = 1 kg \cdot 2,0 \frac {m}{s} = +2 \frac {kg m}{s}}$
Impuls des Wagens B =
$\mathrm {Masse \cdot Geschwindigkeit = 4 kg \cdot -3,0 \frac {m}{s} = -12 \frac {kg m}{s}}$
Also:
Gesamtimpuls der Wagen A und B = $\mathrm {-10 \frac {kg m}{s}}$.
Nach dem Zusammenstoß:
Gesamtimpuls der Wagen A und B = $\mathrm {-10 \frac {kg m}{s}}$ (wie oben)
Also:
kombinierte Masse $\cdot$ Geschwindigkeit = $\mathrm {-10 \frac {kg m}{s}}$
Damit:
$\mathrm {5 kg \cdot Geschwindigkeit = -10 \frac {kg m}{s} \ \big| \ \div 5 kg}$
Also:
Geschwindigkeit der Wagen = $\mathrm {\frac {-10 \frac {kg m}{s}}{5 kg} = -2 \frac {m}{s}}$
Deshalb haben beide Wagen eine Geschwindigkeit von $2 m \tfrac {m}{s}$ und bewegen sich nach links.
Impuls und Energie
Bewegliche Objekte haben kinetische Energie (gemessen in Joule). Bei einer Kollision kann sich ein Teil der Energie in andere Formen umwandeln. Wenn eine Kollision elastisch ist, ist die gesamte kinetische Energie der bewegten Objekte vor der Kollision gleich der Energie nach der Kollision. Mit anderen Worten, es gibt einen "perfekten Zusammenstoß". Allerdings laufen die meisten Kollisionen nicht so ab. Die gesamte kinetische Energie ist nach der Kollision weniger als davor. Hier wird nämlich die "fehlende" Energie in Wärme umgewandelt (Wärmeenergie).
Fragen
Antworten können aufgeklappt werden
Vor dem Versuch:
a) Wie groß ist der Gesamtimpuls beider Autos?
Nach Entspannen der Feder:
b) Wie groß ist der Gesamtimpuls beider Autos?
c) Wie groß ist der Impuls des Autos mit 2 kg Masse?
d) Wie groß ist der Impuls des Autos mit 3 kg Masse?
e) Wie groß ist die Geschwindigkeit des Autos mit 3 kg Masse?
Richtig ist:
a) 0 $\mathrm {\tfrac {kg m}{s}}$
b) 0 $\mathrm {\tfrac {kg m}{s}}$
c) 12 $\mathrm {\tfrac {kg m}{s}}$ nach links
d) 12 $\mathrm {\tfrac {kg m}{s}}$ nach rechts
e) 4 $\mathrm {\tfrac {m}{s}}$ nach rechts
Vor dem Zusammenstoß:
a) Wie groß ist der Impuls des 16kg-Objekts?
b) Wie groß ist der Impuls des 4kg-Objekts?
c) Wie groß ist der Gesamtimpuls beider Objekte?
Nach dem Zusammenstoß:
d) Wie groß ist der Gesamtimpuls beider Objekte?
e) Wie groß ist die Geschwindigkeit der Objekte?
Richtig ist:
a) 80 $\mathrm {\tfrac {kg m}{s}}$ nach rechts
b) 20 $\mathrm {\tfrac {kg m}{s}}$ nach links
c) 60 $\mathrm {\tfrac {kg m}{s}}$ nach rechts
d) 60 $\mathrm {\tfrac {kg m}{s}}$ nach rechts
e) 3 $\mathrm {\tfrac {m}{s}}$ nach rechts