Kraft, Masse und Beschleunigung
Trägheit und Masse
Wenn sich ein Objekt im Ruhezustand befindet, braucht es eine Kraft, um es zu bewegen. Wenn es sich bewegt, braucht es eine Kraft, um es schneller zu machen, langsamer zu machen oder oder es in eine andere Richtung zu lenken. Also versuchen alle Objekte einer Geschwindigkeitsänderung zu widerstehen - auch wenn die Geschwindigkeit Null ist. Dieser Widerstand gegen die Geschwindigkeitsänderung heißt Trägheit. Je mehr Masse etwas hat, desto mehr Trägheit hat es.

Jede Geschwindigkeitsänderung ist eine Beschleunigung. Also: je mehr Masse etwas hat, desto schwieriger ist es, es zu beschleunigen.
Resultierende Kraft
In der Abbildung links sind die beiden Kräfte sind nicht im Gleichgewicht. Gemeinsam sind sie gleichbedeutend mit einer einzigen Kraft. Diese wird als die resultierende Kraft bezeichnet.
| Diese beiden Kräfte..... |
 |
| sind äquivalent zu einer einzigen Kraft (5 - 3) N |
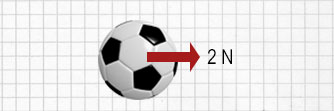 |
| Diese Kraft nennt man resultierende Kraft |
Wenn Kräfte ausgeglichen sind, ist die resultierende Kraft Null und es gibt keine Beschleunigung. Jede andere resultierende Kraft bewirkt eine Beschleunigung - in der gleichen Richtung wie die resultierende Kraft.
Die Beziehung zwischen Kraft, Masse und Beschleunigung
Es besteht eine Verbindung zwischen der resultierenden Kraft, die auf eine Masse wirkt und der daraus resultierenden Beschleunigung. Beispielsweise:
| Wenn die resultierende Kraft... | auf diese Masse wirkt... | ist dies die Beschleunigung |
| $\mathrm {1 \ N}$ | $\mathrm {1 \ kg}$ | $\mathrm {1 \ \frac {m}{s^2}}$ |
| $\mathrm {2 \ N}$ | $\mathrm {2 \ kg}$ | $\mathrm {1 \ \frac {m}{s^2}}$ |
| $\mathrm {4 \ N}$ | $\mathrm {2 \ kg}$ | $\mathrm {2 \ \frac {m}{s^2}}$ |
| $\mathrm {6 \ N}$ | $\mathrm {2 \ kg}$ | $\mathrm {3 \ \frac {m}{s^2}}$ |
In allen Fällen gilt: Resultierende Kraft = Masse $\cdot$ Beschleunigung. Schreibweise:
$F \ = \ m \ \cdot \ a$
Symbole und Einheiten:
- F = Kraft in Newton (N)
- m = Masse in Kilogramm (kg)
- a = Beschleunigung in Meter / Sekunde2 ($\mathrm {\frac {m}{s^2}}$)
Diese Beziehung zwischen Kraft, Masse und Beschleunigung wird manchmal Zweites newtonsche Gesetz der Bewegung genannt.
Beispiel:
Wie groß ist die Beschleunigung des Modellwagens unten?
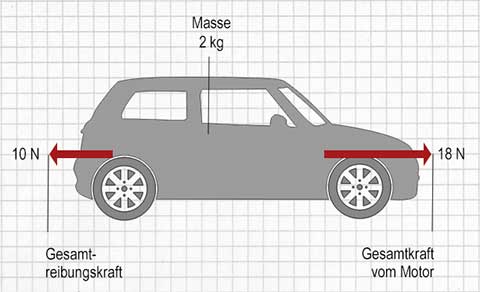
Bestimme als erstes die resultierende Kraft, die auf das Auto wirkt. Die Kraft von $\mathrm {18 \ N}$ nach rechts, kombiniert mit der Kraft von $\mathrm {10 \ N}$ nach links, entspricht einer Kraft von $\mathrm {(18-10) \ N}$ nach rechts. Folglich beträgt die resultierende Kraft $\mathrm {8 \ N}$.
Anschließend kannst du die Beschleunigung berechnen wenn:
$F \ = \ \mathrm {8 \ N}$
und
$m \ = \ \mathrm {2 \ kg}$.
Die entsprechende Formel lautet:
$F \ = \ m \ \cdot \ a$
Also:
$\mathrm {8 \ = \ 2a}$ (Der Einfachheit halber unter Weglassung der Einheiten)
Umgestellt ergibt sich:
$a \ = \ 4$
und somit beträgt die Beschleunigung des Autos
$\mathrm {4 \ \tfrac {m}{s^2}}$.
Definition der Einheit Newton (N)
Eine Kraft von 1 N, die auf 1 kg Masse wirkt, erzeugt eine Beschleunigung von 1 $\mathsf {\tfrac {m}{s^2}}$. Diese einfache Aussage ist kein Zufall. Sie ergibt sich der Art, wie das Newton definiert ist:
1 Newton ist die Kraft, die erforderlich ist, um einer Masse von 1 Kilogramm eine Beschleunigung von 1 $\mathsf {\tfrac {m}{s^2}}$ zu geben.