Eulersche Gleichungen (Kreiseltheorie): Unterschied zwischen den Versionen

Breaking News
Zufallsbild: David Mark / Pixabay

Eulersche Gleichungen (Kreiseltheorie): Unterschied zwischen den Versionen

imported>Sprachpfleger
 
imported>KnightMove
(BKH ist bei Klammerlemma unnötig)
 
Zeile 1: Zeile 1:
{{Dieser Artikel | erläutert die Eulerschen Kreiselgleichungen, zu anderen Bedeutungen siehe [[Eulersche Gleichungen]].}}
Die '''Euler’schen Kreiselgleichungen''' oder uneindeutig '''Euler’schen Gleichungen''' sind [[Bewegungsgleichung]]en für die [[Rotation (Physik)|Rotation]] eines [[Starrer Körper|starren Körpers]]. Es sind die Komponenten des für den Starrkörper in seinem [[Hauptträgheitsachse|Hauptachsensystem]] aufgeschriebenen [[Drallsatz]]es und stellen die wichtigste Grundgleichung der [[Kreiseltheorie]] dar.


Die '''eulerschen Kreiselgleichungen''' oder kurz '''eulerschen Gleichungen''' sind [[Bewegungsgleichung]]en für die [[Rotation (Physik)|Rotation]] eines [[Starrer Körper|starren Körpers]]. Es sind drei gekoppelte [[Differentialgleichung]]en für die Komponenten der [[Winkelgeschwindigkeit]] des Kreisels im körperfesten (mitrotierenden) Koordinatensystem, dessen Achsen die [[Hauptträgheitsachse]]n sind.
Wird der Körper einem [[Drehmoment]] ausgesetzt, entwickeln sich [[Kreiselwirkung]]en, die versuchen, die Eigendrehung mit der erzwungenen Drehung in Deckung zu bringen<ref>Grammel (1920), S. 70.</ref>. Die Kreiselwirkungen sind die summierten Drehmomente der [[Euler-Kraft|Eulerkräfte]] und [[Zentrifugalkraft|Zentrifugalkräfte]] an allen [[Massenpunkt]]en des Körpers. Das Moment und die Kreiselwirkungen befinden sich im [[Dynamisches Gleichgewicht (Technische Mechanik)|dynamischen Gleichgewicht]], was die Kreiselgleichungen ausdrücken:
 
Die eulerschen Kreiselgleichungen sind nicht zu verwechseln mit den [[Eulersche Winkel|eulerschen Winkeln]], die die Orientierung eines körperfesten [[Koordinatensystem]]s in Bezug auf ein raumfestes Koordinatensystem beschreiben. Des Weiteren werden die Bewegungsgleichungen [[Ideale Flüssigkeit|idealer Flüssigkeiten]] in der [[Strömungsmechanik]] ebenfalls als [[Eulersche Gleichungen (Strömungsmechanik)|eulersche Gleichungen]] bezeichnet.
 
== Die eulerschen Kreiselgleichungen ==
In dem mit dem Körper rotierenden Hauptachsensystem lauten die eulerschen Kreiselgleichungen


{{Anker| Kreiselgleichungen}}
:<math>\begin{align}
:<math>\begin{align}
M_1=&I_1\dot{\omega}_1+(I_3-I_2)\omega_2\omega_3
M_1 =& \Theta_1\dot{\omega}_1+(\Theta_3-\Theta_2)\omega_2\omega_3
= \dot L_1+\left(\frac{1}{\Theta_2}-\frac{1}{\Theta_3}\right)L_2L_3
\\
\\
M_2=&I_2\dot{\omega}_2+(I_1-I_3)\omega_3\omega_1
M_2 =& \Theta_2\dot{\omega}_2+(\Theta_1-\Theta_3)\omega_3\omega_1
= \dot L_2+\left(\frac{1}{\Theta_3}-\frac{1}{\Theta_1}\right)L_3L_1
\\
\\
M_3=&I_3\dot{\omega}_3+(I_2-I_1)\omega_1\omega_2.
M_3 =& \Theta_3\dot{\omega}_3+(\Theta_2-\Theta_1)\omega_1\omega_2
= \dot L_3+\left(\frac{1}{\Theta_1}-\frac{1}{\Theta_2}\right)L_1L_2
\end{align}</math>
\end{align}</math>


mit
Darin sind jeweils für <math>k = 1, 2, 3</math>
* ''ω''<sub>1,2,3</sub>: Winkelgeschwindigkeiten um die Hauptachsen
: <math>M_k</math> die von außen angreifenden [[Drehmoment]]e,
* ''I''<sub>1,2,3</sub>: Hauptträgheitsmomente um den [[Massenmittelpunkt]]
: <math>\Theta_k</math> die [[Hauptträgheitsmoment]]e,
* ''M''<sub>1,2,3</sub>: im Massenmittelpunkt angreifende [[Drehmoment]]e und
: <math>L_k = \Theta_k \omega_k</math> die [[Drehimpuls]]e,
* der [[Punkt (Oberzeichen)#Als wissenschaftliches Symbol|aufgesetzte Punkt]] bezeichnet die Zeitableitung, sodass <math>\dot{\omega}_{1,2,3}</math> [[Winkelbeschleunigung]]en um die Hauptachsen darstellen.
: <math>\omega_k</math> die [[Winkelgeschwindigkeit]]en und
: <math>\dot\omega_{k}</math> die [[Winkelbeschleunigung]]en
im Hauptachsensystem. Gelegentlich wird auch die dazu gehörige Vektorgleichung<ref>In der [[Formelsammlung Tensoralgebra#Kreuzprodukt eines Vektors mit einem Tensor|Tensoralgebra]] kann auf Klammerungen verzichtet werden:<br />
:<math>(\vec L\cdot\mathbf{\Theta}^{-1})\times\vec L
=\vec L\cdot(\mathbf{\Theta}^{-1}\times\vec L)
=\vec L\cdot\mathbf{\Theta}^{-1}\times\vec L</math></ref>


Die in den Winkelgeschwindigkeiten quadratischen Terme repräsentieren Trägheitskräfte im rotierenden Bezugssystem. Wenn die Bewegung bekannt ist, dann können aus diesen Gleichungen die Momente berechnet werden, die am Körper in seinem Massenmittelpunkt eingeleitet werden müssen, damit der Körper die vorgegebene Bewegung ausführt.
:<math>\vec M=\mathbf{\Theta}\cdot\dot{\vec\omega}
+\vec\omega\times\mathbf{\Theta}\cdot\vec\omega
= \frac{\mathrm{d}_r}{\mathrm{d}t}\vec L
+\vec L\cdot\mathbf{\Theta}^{-1}\times\vec L
</math>


Bei einer ebenen Bewegung, beispielsweise in der 1-2-Ebene, entfallen Drehungen und Momente um die 1-und 2-Achsen, und die Gleichungen reduzieren sich auf
mit dem [[Trägheitstensor]] <math>\mathbf{\Theta}</math> als Euler’sche Kreiselgleichung angegeben. Hier bildet „·“ die [[Formelsammlung Tensoralgebra#Vektortransformation|Vektortransformation]], „ד das [[Kreuzprodukt]] und <math>\tfrac{\mathrm{d}_r}{\mathrm{d}t}</math> die [[Zeitableitung#Relative Zeitableitung|relative Zeitableitung]] im Hauptachsensystem.


:<math>M_3=I_3\ddot\varphi\,,</math>
Die Drehmomente, Hauptträgheitsmomente und Drehimpulse werden mit einem Bezugspunkt berechnet, für den sich der [[Massenmittelpunkt]] oder ein unbeschleunigter, in einem [[Inertialsystem]] ruhender Stützpunkt eignen, siehe [[Drallsatz#Drallsatz am Starren Körper|Drallsatz am starren Körper]].


wenn ''φ'' der Drehwinkel um die 3-Achse ist.
Die ersten Summanden auf den rechten Seiten, bestehend aus den Winkelbeschleunigungen und Drehimpulsänderungen, resultieren aus den Kreiselwirkungen der Euler-Kräfte und die anderen, in den Winkelgeschwindigkeiten und Drehimpulsen quadratischen Terme berücksichtigen die Kreiselwirkungen der Zentrifugalkräfte. Wenn die Bewegung bekannt ist, dann können aus diesen Gleichungen die Momente berechnet werden, die im Bezugspunkt eingeleitet werden müssen, damit der Körper die vorgegebene Bewegung ausführt.


Die eulerschen Kreiselgleichungen folgen aus der [[Drehimpuls|Drehimpulsbilanz]] eines starren Körpers um seinen Massenmittelpunkt
Die Kreiselgleichungen wurden von [[Leonhard Euler]] 1750 aufgestellt und später zum [[Drallsatz]] weiterentwickelt.<ref name="truesdell" />


:<math>\vec{M}=\mathbf{I}\cdot\dot{\vec{\omega}}+\vec{\omega}\times\mathbf{I}\cdot\vec{\omega}</math>
== Spezialfälle ==
=== Euler-Poisson-Gleichungen ===
{{Hauptartikel| Euler-Poisson-Gleichungen}}
Die Euler-Poisson-Gleichungen sind die spezifischen Kreiselgleichungen für den [[Schwerer Kreisel|schweren Kreisel]], bei dem das äußere Moment von der [[Schwerkraft]] herrührt. Die klassische [[Kreiseltheorie]] ist fast ausschließlich dem schweren Kreisel mit Stützpunkt gewidmet und es wurde viel Aufwand in das Auffinden exakter Lösungen gesteckt. Eine Auflistung einiger dieser Lösungen<ref>Magnus (1971), S. 109.</ref> findet sich im Hauptartikel.


wobei <math>\vec{M}</math> das im Massenmittelpunkt angreifende [[Drehmoment]] ist, <math>\vec{\omega}</math> die Winkelgeschwindigkeit und <math>\mathbf{I}</math> der [[Trägheitstensor]] bezüglich des Massenmittelpunkts ist. Gelegentlich wird auch diese allgemeine Gleichung, die in jedem Koordinatensystem gilt, als eulersche Kreiselgleichung benannt. Im körperfesten Hauptachsensystem <math>\hat{g}_{1,2,3}</math> als speziellem lokalem Bezugssystem ist der Trägheitstensor zeitlich konstant und hat [[Diagonalmatrix|Diagonalgestalt]]:
=== Kugelkreisel ===
Ein [[Kreisel#Einteilung|Kugelkreisel]] ist ein Kreisel mit drei identischen Hauptträgheitsmomenten Θ, sodass sich die Kreiselgleichungen dann auf


:<math>\mathbf{I}
:<math>\vec{M}=\Theta\dot{\vec\omega}</math>
=\sum_{i=1}^3 I_i\hat{g}_i\otimes\hat{g}_i
=\begin{pmatrix}I_1&0&0\\0&I_2&0\\0&0&I_3\end{pmatrix}_{\hat{g}_i\otimes\hat{g}_j}
\,.</math>


Das Rechenzeichen „<math>\otimes</math>“ bildet das [[Dyadisches Produkt|dyadische Produkt]] der Basisvektoren. Die Diagonalglieder ''I''<sub>1,2,3</sub> sind die Hauptträgheitsmomente, die sich aus der Lösung des [[Eigenwertproblem]]s des Trägheitstensors berechnen. In diesem System ergeben sich aus der Drehimpulsbilanz die besonders einfachen, oben angegebenen Komponentengleichungen.
reduzieren. Die Winkelbeschleunigung ist beim Kugelkreisel also parallel zum angreifenden Moment. Beim Kugelkreisel sind die [[Fliehkraft|Fliehkräfte]] im Körper immer im [[Mechanisches Gleichgewicht|mechanischen Gleichgewicht]]. Ein Vergleich mit den [[Bewegungsgleichung]]en bei einer [[Translationsbewegung]] zeigt, dass der Kugelkreisel das genaue Analogon des [[Massenpunkt]]s bei [[Rotation (Physik)|Rotationsbewegungen]] ist.


{| class="wikitable mw-collapsible mw-collapsed"
=== Ebene Bewegungen ===
|-
Bei einer ebenen Bewegung um eine [[Hauptträgheitsachse]], beispielsweise die 3-Achse, entfallen Drehungen und Momente um die 1- und 2-Achsen, und die Gleichungen reduzieren sich auf
| Herleitung im Koordinatenraum
|-
! Von der koordinatenfreien Vektorgleichung zur Koordinatengleichung
|-
| Die eulerschen Kreiselgleichungen folgen aus dem [[Drehimpuls#Eulerscher Drehimpulssatz|Drehimpulssatz]], der gegeben ist durch<br />
<math>\dot{\vec L}=\vec{M}</math>,<br />
wobei <math>\vec L</math> der Drehimpuls und <math>\vec M</math> die Summe aller von außen auf den Körper wirkenden [[Drehmoment]]e im Massenmittelpunkt ist. Setzt man in diese Gleichung die Formel für den (Eigen-)Drehimpuls <math>\vec{L} =\mathbf{I}\cdot\vec\omega</math> mit dem [[Trägheitstensor]] <math>\mathbf{I}</math> bezüglich des Massenmittelpunkts und der Winkelgeschwindigkeit <math>\vec\omega</math> ein, erhält man<br />
<math>\frac{\mathrm{d}}{\mathrm{d}t}\left(\mathbf{I}\cdot\vec\omega\right)=\vec{M}</math>.<br />
Diese Vektorgleichung gilt in jedem Koordinatensystem, aber nur in einem körperfesten sind die Komponenten des Trägheitstensors zeitunabhängig. Die Herleitung der Kreiselgleichungen mittels Vektor/Tensor-Rechnung kann unter [[Drehimpuls#Drehimpulsbilanz am starren Körper|Drehimpulsbilanz am starren Körper]] nachgeschlagen werden. Hier soll der Nachweis im Koordinatenraum angegeben werden.<br />
Es wird ein körperfestes Koordinatensystem mit [[Orthonormalbasis]] <math>\hat{g}_{1,2,3}</math> definiert, sodass die Komponenten <math>I^{ij}_{\rm L}</math> des Trägheitstensors <math>\mathbf{I}=I^{ij}_{\rm L}\hat{g}_i\otimes\hat{g}_j</math> bezüglich dieses Basissystems zeitunabhängig sind. In diesem Abschnitt ist die [[Einsteinsche Summenkonvention]] anzuwenden, der zufolge über in einem Produkt doppelt vorkommende Indizes –&nbsp;hier ''i'' und ''j''&nbsp;– von eins bis drei zu summieren ist. Im Inertialsystem rotieren die Vektoren <math>\hat{g}_{1,2,3}</math>. Durch Darstellung des Trägheitstensors im Inertialsystem mit [[Standardbasis]] <math>\hat{e}_{1,2,3}</math> werden die Komponenten des Trägheitstensors des Starrkörpers durch die Rotation im Allgemeinen zeitabhängig:<br />
<math>\begin{align}
\mathbf{I}=&I^{ij}_{\rm L}\hat{g}_i(t)\otimes\hat{g}_j(t)=I^{ij}(t)\hat{e}_i\otimes\hat{e}_j
\\
\rightarrow I^{kl}
=&\hat{e}_k\cdot\mathbf{I}\cdot\hat{e}_l
=\hat{e}_k\cdot I^{ij}_{\rm L}\hat{g}_i\otimes\hat{g}_j\cdot\hat{e}_l
=(\hat{e}_k\cdot\hat{g}_i)I^{ij}_{\rm L}(\hat{g}_j\cdot\hat{e}_l)
\end{align}</math><br />
Weil die Basis <math>\hat{g}_{1,2,3}</math> durch eine Drehung aus der Standardbasis hervorgeht, ist die [[Transformationsmatrix]] ''R'' mit Komponenten <math>R_{ij}=\hat{e}_i\cdot\hat{g}_j</math> eine [[Drehmatrix]] und es gilt <math>RR^\top=E</math> mit der [[Einheitsmatrix]] ''E'' und dem Zeichen „┬“ für die [[Transponierte Matrix|Transposition]]. Mit der Transformationsmatrix kann die obige Beziehung zwischen den Komponenten des Trägheitstensors als Matrizengleichung geschrieben werden:<br />
<math>I=RI_{\rm L}R^\top.</math><br />
Darin sind <math>I</math> und <math>I_{\rm L}</math> 3×3-Matrizen mit den Komponenten <math>I^{ij}</math> bzw. <math>I^{ij}_{\rm L}</math>. Eine analoge Transformationsbeziehung gilt auch für andere Matrizen, beispielsweise: <math>\Omega=R\Omega_LR^\top</math>, wobei der Index L das lokale, körperfeste Koordinatensystem anzeigt. Für einen Vektor lautet die Transformationsabbildung:<br />
<math>\vec v=v_i\hat{e}_i= v^j_{\rm L}\hat{g}_j
\quad\rightarrow\quad
v_i=\hat{e}_i\cdot\vec v=(\hat{e}_i\cdot\hat{g}_j) v^j_{\rm L}
\quad\rightarrow\quad
v=R v_{\rm L}
\,.</math><br />
Darin sind <math>v</math> und <math>v_{\rm L}</math> Spaltenmatrizen mit den Komponenten <math>v_{1,2,3}</math> bzw. <math>v^{1,2,3}_{\rm L}</math> des Vektors im Inertial-bzw. körperfesten System. Weil die Vektoren und Tensoren auf diese Weise Matrizen zugeordnet werden und dann buchstäblich ihrer Basis beraubt sind, sind die mit den Matrizen aufgestellten Gleichungen nicht mehr koordinatenunabhängig. Üblicher Weise werden Spaltenmatrizen ebenfalls als Vektoren bezeichnet und mit Pfeil notiert, was im Folgenden auch geschehen soll.
|-
! Herleitung der Drehimpulsbilanz im Koordinatenraum
|-
| Setzt man diese Transformationsabbildung vom Inertialsystem ins lokale Bezugssystem in die Drehimpulsbilanz ein, so ergibt sich die Matrizengleichung:<br />
<math>\frac{\mathrm{d}}{\mathrm{d}t}\left(I\vec\omega\right)
=\frac{\mathrm{d}}{\mathrm{d}t}\left(RI_{\rm L}R^\top\vec\omega\right)
=\dot R I_{\rm L} R^\top\vec\omega+R I_{\rm L}\dot R^\top\vec\omega+I\dot{\vec\omega}=
\dot R R^\top I\vec\omega+I R\dot R^\top\vec\omega+I\dot{\vec\omega}
=\vec M\,.</math><br />
Dabei wurden wie üblich Punkte als abkürzende Schreibweise für Zeitableitungen benutzt. Da <math>R</math> orthogonal ist, gilt <math>E=RR^\top</math>, wobei ''E'' die Einheitsmatrix bezeichnet. Leitet man diese Gleichung nach der Zeit ab, erhält man<br />
<math>O=\frac{\mathrm{d}}{\mathrm{d}t}E
=\frac{\mathrm{d}}{\mathrm{d}t}\left(RR^\top\right)=\dot{R}R^\top+R\dot{R}^\top,
</math><br />
mit der [[Nullmatrix]] ''O'', woraus folgt, dass die Matrix <math>\Omega:=\dot{R}R^\top =-R\dot{R}^\top=-\left(\dot{R}R^\top\right)^\top</math> schiefsymmetrisch ist. Die Bedeutung dieser Matrix erkennt man, wenn man die Transformation <math>\vec{a} = R\vec{a}_{\rm L}</math> eines beliebigen konstanten körperfesten Vektors <math>\vec a_{\rm L}</math> ins Inertialsystem nach der Zeit ableitet. Unter Berücksichtigung, dass <math>\vec{a}_{\rm L}</math> konstant ist, erhält man:<br />
<math>\dot{\vec{a}} =\dot R\vec{a}_{\rm L}=\dot R R^\top R\vec{a}_{\rm L} =\Omega\vec{a}\,.</math><br />
Vergleicht man die letzte Gleichung mit der Formel <math>\dot{\vec{a}} =\vec\omega\times\vec{a}</math> für die [[Winkelgeschwindigkeit|Bahngeschwindigkeit eines sich drehenden Vektors]] <math>\vec{a}</math>, erkennt man, dass <math>\Omega=\dot R\,R^\top</math> gerade die zum Kreuzprodukt <math>\vec{a}\in\mathbb{R}^3\mapsto\vec{\omega}\times\vec{a}=[\vec{\omega}]_\times\cdot\vec{a}</math> gehörige schiefsymmetrische [[Kreuzprodukt#Kreuzproduktmatrix|Kreuzproduktmatrix]] <math>[\vec{\omega}]_\times</math> ist. Damit lassen sich <math>\dot R\,R^\top=\Omega</math> und <math>R\,\dot{R}^\top=-\Omega</math> in der letzten Gleichung für <math>\vec{M}</math> durch das Kreuzprodukt mit der Winkelgeschwindigkeit <math>\vec\omega</math> ersetzen:<br />
<math>
\vec{M}=\vec{\omega}\times\left(I\vec {\omega}\right)-I\left(\vec\omega\times\vec\omega\right)+I\dot{\vec\omega}
</math><br />
Mit <math>\vec{\omega}\times\vec{\omega}=\vec{0}</math> ergibt sich daraus<br />
<math>\vec{M} =\vec{\omega}\times\left(I\vec {\omega}\right)+I\dot{\vec\omega}\,.</math><br />
Diese Gleichung wurde hier für die Koordinaten im Inertialsystem hergeleitet, in dem die Koeffizientenmatrix <math>I</math> des Trägheitstensors zeitveränderlich sein kann.<br />
Bei einer Transformation ins lokale Bezugssystem L ist die Zeitableitung von <math>\vec\omega</math> zu berücksichtigen. Mit <math>\vec{\omega}=R\vec{\omega}_{\rm L}</math> ergibt sich<br />
<math>\dot{\vec{\omega}}
=\dot R\vec{\omega}_{\rm L}+R\dot{\vec{\omega}}_{\rm L}
=\dot R R^\top R\vec{\omega}_{\rm L}+R\dot{\vec\omega}_{\rm L}
=\vec{\omega}\times\vec{\omega}+R\dot{\vec\omega}_{\rm L}
= R\dot{\vec{\omega}}_{\rm L}.
</math><br />
Das heißt, die Zeitableitung des in mitbewegte Koordinaten transformierten Winkelgeschwindigkeitsvektors ist gerade die transformierte Winkelbeschleunigung.<br />
Damit lässt sich die letzte Gleichung für <math>\vec{M}</math> direkt in Hauptachsenkoordinaten übertragen.<br />
<math>\vec{M}_{\rm L} =\vec{\omega}_{\rm L}\times\left(I_{\rm L}\vec {\omega}_{\rm L}\right)+I_{\rm L}\dot{\vec\omega}_{\rm L}\,.</math><br />
Im kräftefreien Fall ist <math>\vec{M}_{\rm L} =\vec0\,.</math>
|-
! Alternative Herleitung
|-
| Sei <math>\vec{a}_{\rm L}</math> eine (beliebige) zeitabhängige vektorwertige Größe in lokalen Koordinaten (Index L) und <math>R</math> die Rotationsmatrix für die Transformation <math>\vec{a}=R\vec{a}_{\rm L}</math> von lokalen Koordinaten in ein Inertialsystem. Die zu <math>R</math> gehörige Winkelgeschwindigkeit in lokalen Koordinaten sei <math>\vec{\omega}_{\rm L}</math>. Die Zeitableitung der Transformationsvorschrift <math>\vec{a}=R\vec{a}_{\rm L}</math> lässt sich in der Form<br />
<math>\dot{\vec{a}} = R\left(\vec{\omega}_{\rm L}\times\vec{a}_{\rm L}+\dot{\vec{a}}_{\rm L}\right)</math><br />
darstellen. Wendet man diese Vorschrift auf den Drehimpulssatz<br />
<math>\vec{M} =\frac{\mathrm{d}}{\mathrm{d}t}\vec{L}</math><br />
mit der Darstellung des Drehimpulses im lokalen Bezugssystem <math>\vec{L}=R\vec{L}_{\rm L}</math> an, so erhält man<br />
<math>\vec{M}_{\rm L} =\vec{\omega}_{\rm L}\times\vec{L}_{\rm L}+\dot{\vec{L}}_{\rm L}.</math><br />
Setzt man <math>\vec{L}_{\rm L}=I_{\rm L}\vec{\omega}_{\rm L}</math> mit der konstanten Koeffizientenmatrix <math>I_{\rm L}</math> des Trägheitstensors in Hauptachsendarstellung ein, so ergibt sich daraus die eulersche Gleichung<br />
<math>\vec{M}_{\rm L}
=\vec{\omega}_{\rm L}\times\left(I_{\rm L}\,\vec{\omega}_{\rm L}\right)+I_{\rm L}\dot{\vec{\omega}}_{\rm L}.
</math>
|-
! Nachtrag
|-
| Nachträglich soll noch eine kurze Begründung für die Gleichung <math>\dot{\vec{a}} = R\left(\vec{\omega}_{\rm L}\times\vec{a}_{\rm L}+\dot{\vec{a}}_{\rm L}\right)</math> gegeben werden.<br />
Dabei hilft eine kurze Vorüberlegung zur Transformation des Kreuzproduktes. Seien <math>\vec{a},\vec{b},\vec{c}\in\mathbb{R}^3</math> drei beliebige Vektoren. Der durch <math>\vec{a},\vec{b},\vec{c}</math> aufgespannte Spat ändert unter einer [[Drehgruppe|Rotation]] <math>R\in\operatorname{SO}(3)</math> sein Volumen nicht. Es gilt also <math>\vec{a}^\top\left(\vec{b}\times\vec{c}\right)
=(R\vec{a})^\top\left((R\vec{b})\times(R\vec{c})\right)
=\vec{a}^\top\left(R^\top\left((R\vec{b})\times(R\vec{c})\right)\right).</math> Da in dieser Gleichung <math>\vec{a}</math> beliebig ist, gilt auch <math>\vec{b}\times\vec{c} = R^\top\left((R\vec{b})\times(R\vec{c})\right)</math>, also <math>R\left(\vec{b}\times\vec{c}\right) = (R\vec{b})\times(R\vec{c})</math>.<br />
Die Zeitableitung von <math>\vec{a}=R\vec{a}_{\rm L}</math> ergibt sich zu<br />
<math>\dot{\vec{a}}
=\dot{R}\vec{a}_{\rm L}+R\dot{\vec{a}}_{\rm L}
=\dot{R} R^\top R\vec{a}_{\rm L}+R\dot{\vec{a}}_{\rm L}
=\vec{\omega}\times\vec{a}+R\dot{\vec{a}}_{\rm L}
</math><br />
und mit der Vorüberlegung zur Transformation des Kreuzproduktes erhält man<br />
<math>\dot{\vec{a}} = R\left(\vec{\omega}_{\rm L}\times\vec{a}_{\rm L}+\dot{\vec{a}}_{\rm L}\right).</math>
|}


== Anwendungen ==
:<math>M_3=\Theta_3\ddot\varphi\,,</math>
=== Rotierender Kugelkreisel ===
Ein [[Kreisel#Einteilung|Kugelkreisel]] ist ein Kreisel mit drei identischen Hauptträgheitsmomenten ''I''. Die Kreiselgleichungen reduzieren sich bei einem Kugelkreisel auf


:<math>\vec{M}=I\dot{\vec{\omega}}\,.</math>
wobei ''φ'' der Drehwinkel um die 3-Achse ist.


Die Winkelbeschleunigung ist also parallel zum Moment.
== Lösungen der Kreiselgleichungen bei ebenen Bewegungen ==
Im ebenen Fall sind die Kreiselgleichungen oftmals analytisch lösbar, wofür die beiden folgenden Fälle Beispiele sind.


=== Anstoß einer Billardkugel ===
=== Anstoß einer Billardkugel ===
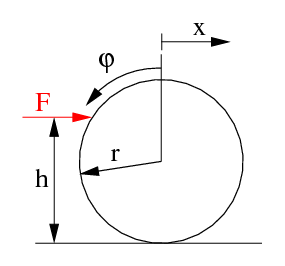
[[Datei:billardstoss.png|mini|Abb. 1: Anstoß einer Billardkugel parallel zur Tischplatte]]
[[Datei:billardstoss.png|mini|Abb. 1: Anstoß einer Billardkugel parallel zur Tischplatte]]
Parallel zur Tischplatte soll eine [[Billardkugel]] mit Radius ''r'', Masse ''m'' und Massenträgheitsmoment ''I'' so angestoßen werden, dass sie nicht über den Tisch rutscht, siehe Abb. 1. Es stellt sich die Frage, in welcher Höhe ''h'' über der Platte die Kraft ''F'' eingeleitet werden muss, damit für das schlupflose Rollen keine Reibkraft am Tisch notwendig ist.
Parallel zur Tischplatte soll eine [[Billardkugel]] mit Radius ''r'', Masse ''m'' und Massenträgheitsmoment Θ so angestoßen werden, dass sie nicht über den Tisch rutscht, siehe Abb.&nbsp;1. Es stellt sich die Frage, in welcher Höhe ''h'' über der Platte die Kraft ''F'' eingeleitet werden muss, damit für das schlupflose Rollen keine Reibkraft am Tisch notwendig ist.
 
Die exzentrisch an der Kugel angreifende horizontale Kraft entwickelt ein Moment ''M''=-(''h-r'')''F'', das die Kugel gemäß der Kreiselgleichung
 
:<math>M=-(h-r)F=I\ddot\varphi</math>


Die exzentrisch an der Kugel angreifende horizontale Kraft entwickelt ein Moment ''M&nbsp;=&nbsp;-(h-r)F'' um den Massenmittelpunkt, das die Kugel gemäß der Kreiselgleichung
:<math>M=-(h-r)F=\Theta\ddot\varphi</math>
in Drehung versetzt. Das Moment ist negativ, weil es entgegen der Zählrichtung des Drehwinkels ''φ'' wirkt. Außerdem beschleunigt die Kraft die Kugel gemäß dem Gesetz „[[Newtonsche Axiome#Zweites newtonsches Gesetz|Kraft gleich Masse mal Beschleunigung]]“:
in Drehung versetzt. Das Moment ist negativ, weil es entgegen der Zählrichtung des Drehwinkels ''φ'' wirkt. Außerdem beschleunigt die Kraft die Kugel gemäß dem Gesetz „[[Newtonsche Axiome#Zweites newtonsches Gesetz|Kraft gleich Masse mal Beschleunigung]]“:


Zeile 160: Zeile 76:
:<math>\ddot x=-r\ddot\varphi</math>
:<math>\ddot x=-r\ddot\varphi</math>


schließt das Gleichungssystem für die drei Unbekannten ''h'', ''φ'' und ''x'' ab. Damit berechnet sich
schließt das Gleichungssystem für die drei Unbekannten ''h, φ'' und ''x'' ab. Damit berechnet sich


:<math>-(h-r)F=I\ddot\varphi=-\frac{I}{r}\ddot x=-\frac{I}{mr}F
:<math>-(h-r)F=\Theta\ddot\varphi=-\frac{\Theta}{r}\ddot x=-\frac{\Theta}{mr}F
\quad\rightarrow\quad
\quad\rightarrow\quad
h=r+\frac{I}{mr}
h=r+\frac{\Theta}{mr}
\,.</math>
\,.</math>


Bei einer massiven homogenen Kugel ist das [[Massenträgheitsmoment#Hauptträgheitsmomente einfacher geometrischer Körper|Massenträgheitsmoment]] <math>I=\tfrac{2}{5}mr^2</math> und somit
Bei einer massiven homogenen Kugel ist das [[Massenträgheitsmoment#Hauptträgheitsmomente einfacher geometrischer Körper|Massenträgheitsmoment]] Θ&nbsp;=&nbsp;{{Bruch|2|5}}mr² und somit


:<math>h=\frac{7}{5}r=\frac{7}{10}d\,,</math>
:<math>h=\frac{7}{5}r=\frac{7}{10}d\,,</math>


wenn ''d'' der [[Durchmesser]] der Kugel ist.
wobei ''d&nbsp;=&nbsp;2r'' der [[Durchmesser]] der Kugel ist.


=== Eine schiefe Ebene hinabrollendes Rad ===
=== Ein eine schiefe Ebene hinabrollendes Rad ===
[[Datei:rotradebene.png|mini|Abb. 2: Ein eine schiefe Ebene hinab rollendes Rad.]]
[[Datei:rotradebene.png|mini|Abb. 2: Ein eine schiefe Ebene hinab rollendes Rad.]]
In einer ebenen Bewegung rolle ein Rad mit Radius ''r'', Masse ''m'' und Massenträgheitsmoment ''I'' eine mit dem Winkel ''α'' geneigte Ebene unter Einfluss einer Schwerebeschleunigung ''g'' hinab, siehe Abb. 2. Weil sich das Rad dabei auch translatorisch bewegt, geht auch seine Masse in die Beschleunigung ein. Die Beschleunigung wächst jedoch, wenn das Massenträgheitsmoment abnimmt.
In einer ebenen Bewegung rolle ein Rad mit Radius ''r'', Masse ''m'' und Massenträgheitsmoment Θ eine mit dem Winkel ''α'' geneigte Ebene unter Einfluss einer Schwerebeschleunigung ''g'' hinab, siehe Abb. 2. Weil sich das Rad dabei auch translatorisch bewegt, geht auch seine Masse in die Beschleunigung ein. Die Beschleunigung wächst jedoch, wenn das Massenträgheitsmoment abnimmt.


Aufgrund des [[schlupf]]losen Abrollens entsteht am Aufstandspunkt des Rades eine Reibkraft ''R'', die das Rad in Drehung versetzt, denn es entspricht einem Moment ''M''=-''r R''. Es ist negativ, weil es entgegen der Zählrichtung des Drehwinkels ''φ'' arbeitet. Damit lautet die Kreiselgleichung im ebenen Fall:
Aufgrund des [[schlupf]]losen Abrollens entsteht am Aufstandspunkt des Rades eine Reibkraft ''R'', die das Rad in Drehung versetzt, denn es entspricht einem Moment ''M''=-''r&nbsp;R'' um den Massenmittelpunkt. Das Moment ist negativ, weil es entgegen der Zählrichtung des Drehwinkels ''φ'' arbeitet. Damit lautet die Kreiselgleichung im ebenen Fall:


:<math>-r R=I\ddot\varphi\,.</math>
:<math>-r R=\Theta\ddot\varphi\,.</math>


Die auf das Rad hangabwärts wirkende Komponente ''F'' der Gewichtskraft ''mg'' hat die Größe ''F''=''mg''sin(''α''). Ihr entgegen steht die Reibkraft, so dass nach dem [[Newtonsche Axiome#Zweites newtonsches Gesetz|zweiten newtonschen Gesetz]] gilt:
Die auf das Rad hangabwärts wirkende Komponente ''F'' der Gewichtskraft ''mg'' hat die Größe ''F''=''mg''sin(''α''). Ihr entgegen steht die Reibkraft, sodass nach dem [[Newtonsche Axiome#Zweites newtonsches Gesetz|zweiten newtonschen Gesetz]] gilt:


:<math>F-R=m\ddot x
:<math>F-R=m\ddot x
Zeile 188: Zeile 104:
\,,</math>
\,,</math>


worin <math>\ddot x</math> die hangabwärts zählende Beschleunigung des Rades und sin die [[Sinus und Kosinus|Sinusfunktion]] ist. Die Bedingung für schlupfloses Rollen <math>\ddot x=-r\ddot\varphi</math> schließt das Gleichungssystem für die drei Unbekannten ''R'', ''φ'' und ''x'' ab, die sich letztendlich ergeben zu:
worin <math>\ddot x</math> die hangabwärts zählende Beschleunigung des Rades und sin die [[Sinus und Kosinus|Sinusfunktion]] ist. Die Bedingung für schlupfloses Rollen <math>\ddot x=-r\ddot\varphi</math> schließt das Gleichungssystem für die drei Unbekannten ''R'', ''φ'' und ''x'' ab und es ergibt sich
 
:<math>\begin{align}
\ddot\varphi=&-\frac{mr^2}{I+mr^2}\frac{g}{r}\sin(\alpha)=-\frac{r}{I+mr^2}F
\\
R=&\frac{I}{I+mr^2}mg\sin(\alpha)=\frac{I}{I+mr^2}F
\\
\ddot x=&\frac{mr^2}{I+mr^2}g\sin(\alpha)=\frac{r^2}{I+mr^2}F
\,.\end{align}</math>


Die maximale Beschleunigung bei gegebenem Gefälle stellt sich ein, wenn sich die Masse des Rades möglichst nahe an seinem Mittelpunkt konzentriert und sich somit das Massenträgheitsmoment minimiert.
:<math>\ddot x=\frac{mr^2}{\Theta+mr^2}g\sin(\alpha)</math>


Ein hangabwärts, reibungsfrei rutschender Klotz erfährt die Beschleunigung <math>\ddot x=g\sin(\alpha)</math>, die größer ist als die des Rades, denn beim Rad wird ein Teil der [[Potentielle Energie|potentiellen Energie]] in [[Rotationsenergie]] umgesetzt, die dann für die Translation fehlt.
Ein hangabwärts, reibungsfrei rutschender Klotz erfährt die Beschleunigung <math>\ddot x=g\sin(\alpha)</math>, die größer ist als die des Rades, denn beim Rad wird ein Teil der [[Potentielle Energie|potentiellen Energie]] in [[Rotationsenergie]] umgesetzt, die dann für die Translation fehlt.


=== Allgemeine Eigenschaften der Bewegung kräftefrei rotierender Kreisel ===
== Beispiel: Fliehkraftpendel ==
Außer in der Schwerelosigkeit kann ein kräftefreier Kreisel in einem Schwerefeld realisiert werden, indem er in seinem Schwerpunkt drehbar, beispielsweise [[Kardanische Aufhängung|kardanisch]] aufgehängt wird.
Ein bemerkenswerter Anwendungsfall der Euler’schen Kreiselgleichungen ist die "Perle auf rotierendem Kreisring im Schwerefeld"<ref name="eckelt">{{Internetquelle
 
| autor=P. Eckelt
==== Erhaltungsgrößen der Bewegung ====
| hrsg=Institut für Theoretische Physik an der Westfälischen Wilhelms-Universität Münster
Die Drehbewegung eines kräftefreien Kreisels unterliegt neben den Kreiselgleichungen noch zwei Bedingungen: zum einen der [[Drehimpulserhaltung]] <math>\vec L= \text{const.}</math> und zum anderen dem [[Energieerhaltungssatz]] <math>E_\mathrm{rot}= \text{const.}</math> Im lokalen körperfesten Hauptachsensystem ausgedrückt lauten diese mit <math>L:=|\vec L|</math>:
| url=http://pauli.uni-muenster.de/tp/fileadmin/lehre/skripte/eckelt/thmech.pdf
| format=PDF
| titel=Theoretische Mechanik
| seiten=11 bis 13
| datum=2000
| zugriff=2016-07-16
| kommentar=siehe auch die dort angegebenen Quellen
}}</ref><ref name="arnold">Arnold (1988), S. 95 f.</ref>, das [[Konisches Pendel|konische]] oder [[Fliehkraftpendel]], denn es hat überraschende Eigenschaften. In Worten der Kreiseltheorie handelt es sich um einen [[Schwerer Kreisel|schweren Kreisel]], der in einem Punkt festgehalten wird und bei dem die Eigendrehung um die Pendelachse durch äußere Momente verhindert und die Präzessionsgeschwindigkeit konstant gehalten wird. Komplexere Eigenschaften treten bei beliebiger Lage des [[Massenmittelpunkt]]s und anfänglicher Ausrichtung der Hauptachsen auf. Vereinfachungen ergeben sich mit Massenmittelpunkt auf der 1-Achse und permanent horizontaler 3-Achse des [[Hauptträgheitsachse| Hauptachsen]]&shy;systems.


:<math>\begin{align}
=== Kinematik ===
L^2
Die in der Kreiseltheorie üblichen [[Kreiseltheorie#Bezugssysteme und Euler-Winkel|Definitionen der Winkel und Winkelgeschwindigkeiten]] werden übernommen. Insbesondere wird die z-Komponente der 2-Achse
=&
(\mathbf{I}\cdot\vec\omega)\cdot(\mathbf{I}\cdot\vec\omega)
=
I^2_1\omega^2_1+I^2_2\omega^2_2+I^2_3\omega^2_3
=
\text{const.}
\\
2E_\mathrm{rot}
=&
\vec\omega\cdot\mathbf{I}\cdot\vec\omega
=
I_1\omega^2_1+I_2\omega^2_2+I_3\omega^2_3
=
\text{const.}
\end{align}</math>
 
Diese beiden Gleichungen stellen mathematisch [[Ellipsoid]]e dar, die erste das [[Trägheitsellipsoid#Drallellipsoid|Drallellipsoid]], die zweite das [[Energieellipsoid]]. Damit beide Ellipsoide gemeinsame Punkte haben können, muss zu jedem Zeitpunkt
 
:<math>2 I_1 E_{\rm rot} \le L^2 \le 2 I_3 E_{\rm rot}</math> oder <math>\frac{L^2}{2I_3}\le E_{\rm rot}\le \frac{L^2}{2I_1}</math>
 
sein, wenn wie üblich die Hauptträgheitsmomente gemäß ''I''<sub>1</sub> < ''I''<sub>2</sub> < ''I''<sub>3</sub> angeordnet sind.
 
Denn ein Punkt, der auf beiden Ellipsoiden liegt, muss die Bedingungen
 
:<math>\begin{align}
1
=&
\frac{1}{L^2}(I_1^2\omega_1^2+I_2^2\omega_2^2+I_3^2\omega_3^2)
=
\frac{1}{2E_{\rm rot}}(I_1\omega_1^2+I_2\omega_2^2+I_3\omega_3^2)
\\
\rightarrow
0
=&
(2E_{\rm rot}I_1-L^2)I_1\omega_1^2
+(2E_{\rm rot}I_2-L^2)I_2\omega_2^2
+(2E_{\rm rot}I_3-L^2)I_3\omega_3^2
\\=&
2\left(E_{\rm rot}-\frac{L^2}{2I_1}\right)I_1^2\omega_1^2
+2\left(E_{\rm rot}-\frac{L^2}{2I_2}\right)I_2^2\omega_2^2
+2\left(E_{\rm rot}-\frac{L^2}{2I_3}\right)I_3^2\omega_3^2
\end{align}</math>


erfüllen. In den letzten beiden Gleichungen sind alle Faktoren bis auf die Klammerausdrücke null oder positiv. Eine nicht-triviale Lösung existiert, wenn in den Gleichungen der kleinste Klammerausdruck nicht positiv und der größte nicht negativ ist. Mit den angenommenen Größenverhältnissen der Hauptträgheitsmomente stellen dies die obigen Schranken für das Drehimpulsbetragsquadrat und die Rotationsenergie sicher. Dann sind die Rotationsenergie und der Drehimpulsbetrag mit einer Drehbewegung des betrachteten Körpers verträglich.
:<math>n_2=\sin(\vartheta)\cos(\varphi)=\cos(\varphi)</math>


==== Geometrische Deutung der Erhaltungsgrößen ====
bei horizontaler 3-Achse (ϑ&nbsp;≡&nbsp;90°) benötigt, die identisch mit der 2-Komponente des [[Einheitsvektor]]s ist, der vertikal nach oben weist. Die Funktionen sin und cos bilden den [[Sinus und Kosinus]].
Eine sinnfällige Darstellung der durch die Energie-und Drehimpulserhaltung definierten Flächen ergibt sich durch Übergang zu den lokalen Komponenten des Drehimpulses, die gemäß ''L''<sub>i</sub>=''I''<sub>i</sub>''ω''<sub>i</sub> das Produkt des Hauptträgheitsmoments mit der entsprechenden Komponente der Winkelgeschwindigkeit sind. Aus der Erhaltung von Energie und Drehimpulsbetrag entsteht das Gleichungssystem:


[[Datei:polhodienaufkugel.png|mini|Abb. 4: Trägerkurven der Lösungen der Kreiselgleichungen mit ''I''<sub>1</sub>=2 [[Kilogramm|kg]] [[Meter|m]]², ''I''<sub>2</sub>=4 kg m² und ''I''<sub>3</sub>=10 kg m². Die Kurven gleicher Rotationsenergie sind mit Werten 1,5…6 [[Newtonmeter|N m]] in 0,5&nbsp;N m Schritten bei einem Drehimpuls <math>|\vec L| = 5 \, \mathrm{N\,m\, s}</math> gezeichnet.]]
Die Winkelgeschwindigkeiten lauten unter den hiesigen Bedingungen:


:<math>\begin{align}
:<math>\begin{align}
\dot{L}_1=&-\left(\frac{1}{I_2}-\frac{1}{I_3}\right)L_2L_3
\mu:=&\dot\psi=\omega_1\sin(\varphi)+\omega_2\cos(\varphi)=\text{const.}
\\
\dot{L}_2=&\left(\frac{1}{I_1}-\frac{1}{I_3}\right)L_3L_1
\\
\dot{L}_3=&-\left(\frac{1}{I_1}-\frac{1}{I_2}\right)L_1L_2.
\\
\\
L^2=& L_1^2+L_2^2+L_3^2=\text{const.}
\dot\vartheta=&\omega_1\cos(\varphi)-\omega_2\sin(\varphi)\equiv0
\\
\\
2E_\mathrm{rot}=&\frac{L_1^2}{I_1}+\frac{L_2^2}{I_2}+\frac{L_3^2}{I_3}=\text{const.}
\omega_1=&\mu\sin(\varphi),\;\omega_2=\mu\cos(\varphi),\;\omega_3=\dot\varphi
\end{align}</math>
\end{align}</math>


Durch die ersten drei Kreiselgleichungen sind die letzten beiden Erhaltungsgleichungen automatisch erfüllt, was durch deren Zeitableitung nachgewiesen werden kann. Der Drehimpuls, der im raumfesten Inertialsystem konstant bleibt, liegt im lokalen, körperfesten, rotierenden Bezugssystem auf einer [[Kugel]], die in Abb. 4 aus drei Richtungen gesehen gezeichnet ist. Denn hier können die Komponenten des Drehimpulses jedweden Punkt der Kugel einnehmen, auch wenn der Drehimpuls im Inertialsystem immer in dieselbe Richtung weist. Die zusätzliche Bedingung der Energieerhaltung zwingt die Komponenten des Drehimpulses auf ein Ellipsoid. Die Schnittmenge von Kugel und Ellipsoid sind geschlossene Kurven (rot und blau im Bild), die [[Kreis]]-, [[Ellipse]]n- oder [[Taco]]-förmig sein können.
Der Winkel ϑ ist unveränderlich, wenn er anfangs keine [[Zeitableitung]] hat und dauerhaft keine Beschleunigung erfährt.


==== Stabilitätsbetrachtungen ====
=== Kinetik ===
Die Kurven gleicher Energie und gleichen Drehimpulses degenerieren zu Punkten, wenn die Rotation um eine der Hauptträgheitsachsen erfolgt. Liegt der Drehimpuls in der Nähe der Hauptträgheitsachse mit dem größten oder dem kleinsten Trägheitsmoment (blaue bzw. rote Punkte im Bild), dann verbleibt er auch in dessen Nähe, denn diese Punkte werden von den Kurven umringt. Deshalb sind diese Drehachsen stabile Drehachsen freier Drehungen. Ihre Schnittpunkte mit dem [[Energieellipsoid]] sind elliptische Fixpunkte einer [[Autonome Differentialgleichung#Qualitative Theorie der Fixpunkte der Differentialgleichung|autonomen Differentialgleichung]].
Die 1- oder Pendelachse trägt im Abstand ''s''&nbsp;>&nbsp;0 vom Fixpunkt den [[Massenmittelpunkt]], dessen [[Gewichtskraft]] ''mg'' somit ein Schweremoment auf das Pendel ausübt. Zusätzlich zu diesem Schweremoment wirken äußere Momente M<sub>1,2</sub> in 1- bzw. 2-Richtung des Hauptachsensystems, um Winkelbeschleunigungen von ϑ und ''μ'' zu unterdrücken. Die Kreiselgleichungen in 1- und 2-Richtung dienen nur der Bestimmung dieser Momente, die hier nicht interessieren. Bemerkenswert ist jedoch, dass diese Drehmomente eine zeitliche Änderung des vertikalen Drehimpulses verursachen<ref name="eckelt"/>, der bei [[Schwerer Kreisel|schweren Kreiseln]] immer konstant ist.


Insoweit die Komponenten des Drehimpulses [[Lipschitz-Stetigkeit|Lipschitz-stetig]] sind, können sich die Trajektorien des Drehimpulses nicht schneiden ([[Satz von Picard-Lindelöf]]). Diese Bedingung ist auf der ''Separatrix'' mit 2 ''I''<sub>2</sub> ''E''<sub>rot</sub> = ''L''² verletzt (im Bild schwarz gestrichelt), wenn wie hier ''I''<sub>2</sub> gemäß ''I''<sub>1</sub> < ''I''<sub>2</sub> < ''I''<sub>3</sub> das mittelgroße Hauptträgheitsmoment ist. Liegt der Drehimpuls genau auf der 2-Achse (schwarzer Punkt), dann verbleibt er dort. Befindet er sich in einem anderen Punkt in der Umgebung des Schnittpunkts, dann kann sich der Drehimpuls vom Schnittpunkt nur entfernen und bleibt auch nicht in der Nähe des Schnittpunkts. Die 2-Achse ist eine ''instabile'' Drehachse, sie trifft das [[Energieellipsoid]] in einem hyperbolischen Fixpunkt oder Sattelpunkt der zugehörigen autonomen Differentialgleichung (siehe auch [[#Stabilität der Bewegung unsymmetrischer Kreisel]] weiter unten).
Um die horizontale 3-Richtung kann das Pendel frei drehen und das Schweremoment in dieser Richtung ist -''mgsn''<sub>2</sub>&nbsp;=&nbsp;-''mgs''&nbsp;cos(''φ''), siehe Kinematik oben und [[Euler-Poisson-Gleichungen]]. Damit liefert die dritte der Kreiselgleichungen


Wenn zwei Hauptträgheitsmomente übereinstimmen, was beim ''symmetrischen'' Kreisel der Fall ist, dann ist das Energieellipsoid ein [[Rotationsellipsoid]], die Schnittkurven mit der Kugel sind dann [[Kleinkreis]]e und die Separatrix wird zu einem [[Großkreis]]. Eine instabile Drehachse existiert dann nicht.
:<math>M_3=-mgs\cos(\varphi)=C\dot\omega_3+(B-A)\omega_1\omega_2</math>


==== Die Bewegungen des Drehimpulses im lokalen Bezugssystem ====
die Bewegungsgleichung
Der Drehimpuls durchwandert diese Kurven – außer die Separatrix – komplett ohne jemals stillzustehen oder gar die Umlaufrichtung zu wechseln. Denn auf den Kurven abseits der Hauptträgheitsachsen verschwindet höchstens eine Komponente des Drehimpulses. Deswegen können die lokalen Geschwindigkeiten <math>\dot{L}_{1,2,3}</math> nicht alle drei auf einmal null sein. Im Sonderfall der Separatrix bildet sich eine aperiodische Bewegung aus, denn der Drehimpuls kann die Schnittpunkte auf der 2-Achse nicht überschreiten. Es zeigt sich, dass sich die Hauptträgheitsachse mit dem mittleren Hauptträgheitsmoment auf einer [[Loxodrome]] asymptotisch der vom Drehimpuls gegebenen Achse nähert, siehe [[#Bewegung auf der Separatrix]] unten.


Wenn die Rotationsenergie abnimmt, beispielsweise durch [[Dissipation]], wird die Drehachse in Richtung der Achse mit dem größten Trägheitsmoment wandern, was im Bild die 3-Achse ist, denn dort berührt das Energieellipsoid mit der kleinsten Energie die Drehimpulskugel.
{{Anker|phipp}}
{{NumBlk|:|<math>
\ddot\varphi=\frac1C[(A-B)\mu^2\sin(\varphi)-mgs]\cos(\varphi)
</math>|*}}


=== Kräftefreier symmetrischer Kreisel ===
Darin sind A, B und C die [[Hauptträgheitsmoment]]e um die 1-, 2- bzw. 3-Achse.
Beim ''symmetrischen'' Kreisel sind [[per definitionem]] zwei der Hauptträgheitsmomente gleich. Ohne Beschränkung der Allgemeinheit wird hier von ''I''<sub>1</sub>=''I''<sub>2</sub>=:''I''<sub>0</sub> und Drehung um die 3-Achse – der [[Figurenachse]] – ausgegangen.


==== Betrachtung im rotierenden Bezugssystem ====
=== Gleichgewichtslagen ===
Beim symmetrischen Kreisel vereinfacht sich die dritte Kreiselgleichung im kräftefreien Fall zu <math>I_3\,\dot{\omega}_3=0</math>, sodass die Winkelgeschwindigkeit <math>\omega_3</math> konstant ist. Die zwei anderen Kreiselgleichungen bilden das lineare [[gewöhnliche Differentialgleichung]]ssystem
Im Gleichgewicht verschwindet in [[#phipp|(*)]] die Winkelbeschleunigung:


:<math>\begin{align}
:<math>C\ddot\varphi=[(A-B)\mu^2\sin(\varphi)-mgs]\cos(\varphi)=0</math>.
0=&
\dot{\omega}_1+\frac{I_3-I_0}{I_0}\omega_2\omega_3
=
\dot{\omega}_1+\Omega\omega_2
\\
0=&
\dot{\omega}_2+\frac{I_0-I_3}{I_0}\omega_3\omega_1
=
\dot{\omega}_2-\Omega\omega_1
\end{align}</math>


mit konstantem Koeffizient <math>\Omega :=\tfrac{I_3-I_0}{I_0}\omega_3</math>. Die allgemeine Lösung dieser Gleichungen ist wie folgt darstellbar:
Anders als beim sich selbst überlassenen [[Lagrange-Kreisel]] ist eine Präzession mit waagerechter Achse (''φ''&nbsp;=&nbsp;0) nicht möglich. Mangels Eigendrehung gibt es hier keine Kreiselwirkung, die das Schweremoment ausgleichen könnte. Das Gleichgewicht mit lotrechter 1-Achse (''φ''&nbsp;=&nbsp;±90°) ist allen Kreiseln zugänglich – auch dem [[Kugelkreisel]], der nur dort Gleichgewicht findet. Bei ''A&nbsp;≠&nbsp;B'' ergeben sich die Gleichgewichtslagen aus


:<math>
:<math>
\begin{pmatrix}\omega_1(t)\\\omega_2(t)\end{pmatrix}
\left[\sin(\varphi)-\frac{mgs}{(A-B)\mu^2}\right]\cos(\varphi)=0
=
\begin{pmatrix}\cos(\Omega\,t)&-\sin(\Omega\,t)\\\sin(\Omega\,t)&\cos(\Omega\,t)\end{pmatrix}
\begin{pmatrix}\omega_1(0)\\\omega_2(0)\end{pmatrix}
</math>
</math>


Die Werte ''ω''<sub>1,2</sub>(0) sind Anfangsbedingungen zur Zeit ''t''=0. Falls ''ω''<sub>3</sub>(0)=0 und/oder ''ω''<sub>1</sub>(0)=''ω''<sub>2</sub>(0)=0 gilt, so bleiben ''ω''<sub>1</sub> und ''ω''<sub>2</sub> konstant und der Kreisel führt eine konstante Drehbewegung aus oder bleibt im Spezialfall ''ω''<sub>1,2,3</sub>(0)=0 in Ruhe.
Wenn ''A&nbsp;-&nbsp;B'' dasselbe Vorzeichen wie sin(''φ'') hat, kann der Term in der eckigen Klammer null werden. Dazu muss


[[Datei:kreiselkegel.png|mini|Abb. 4: Bewegungskomponenten beim kräftefreien Kreisel]]
:<math>|\sin(\varphi)|\le1
Für die Skizzierung der allgemeinen Bewegung wird im Massenmittelpunkt des Kreisels zum Zeitpunkt ''t''=0 ein [[kartesisches Koordinatensystem]] mit x-, y-und z-Achse so gelegt, dass die Figurenachse und die Winkelgeschwindigkeit in der x-z-Ebene liegen, siehe Abb. 4. Der Winkel zwischen der Winkelgeschwindigkeit und der Figurenachse sei ''λ''. Dann ist ''ω''<sub>1</sub>(0)=''ω'' sin(''λ''), ''ω''<sub>2</sub>(0)=0 (in Abb. 4 anders dargestellt) und ''ω''<sub>3</sub>(0)=''ω'' cos(''λ'') mit dem Betrag <math>\omega:=|\vec\omega|</math> der Winkelgeschwindigkeit. Die zu den Winkelgeschwindigkeiten gehörenden Hauptträgheitsachsen werden mit <math>\hat{g}_{1,2,3}</math> bezeichnet.
\quad\Rightarrow\quad
|\mu|\ge\sqrt{\frac{mgs}{|A-B|}}=:\mu_c</math>


Die oben angegebene Lösung der Kreiselgleichungen ergibt mit den getroffenen Anfangsbedingungen:
erfüllt sein. Das Pendel muss eine kritische Drehgeschwindigkeit ''μ''<sub>c</sub> überschreiten, damit diese Gleichgewichtslage abseits der Senkrechten existiert. Beim ''abgeplatteten'' Kreisel weist die 1-Achse im Gleichgewicht nach oben (ist ''A&nbsp;>&nbsp;B'' und sin(''φ'')&nbsp;>&nbsp;0) und beim ''gestreckten'' nach unten (''A&nbsp;<&nbsp;B'' und sin(''φ'')&nbsp;<&nbsp;0).


:<math>
Analog zum [[Symmetrischer Kreisel|symmetrischen Kreisel]] wird das Pendel hier und im folgenden ''abgeplattet'' genannt, wenn ''A&nbsp;>&nbsp;B'', und ''gestreckt'', wenn ''B&nbsp;>&nbsp;A''.
\begin{pmatrix}\omega_1(t)\\\omega_2(t)\end{pmatrix}
=
\begin{pmatrix}\cos(\Omega\,t)&-\sin(\Omega\,t)\\\sin(\Omega\,t)&\cos(\Omega\,t)\end{pmatrix}
\begin{pmatrix}\omega\sin(\lambda)\\0\end{pmatrix}
=
\begin{pmatrix}\omega\sin(\lambda)\cos(\Omega\,t)\\\omega\sin(\lambda)\sin(\Omega\,t)\end{pmatrix}
</math>


Die Amplitude <math>\omega_\bot:=\sqrt{\omega_1^2+\omega_2^2}=\omega|\sin(\lambda)|</math> ist konstant, so dass die Figurenachse und die Winkelgeschwindigkeit immer denselben Winkel, nämlich ''λ'', einschließen. Der Differenzvektor <math>\vec{\omega}_\bot:=\vec\omega-\omega_3\hat{g}_3=\omega_1\hat{g}_1+\omega_2\hat{g}_2</math> hat den Betrag <math>\omega_\bot</math> und rotiert um die Figurenachse mit der [[Drehzahl]] <math>\tfrac{\Omega}{2\pi}</math>. Die Winkelgeschwindigkeit führt daher im körperfesten Hauptachsensystem eine Drehbewegung um die Figurenachse aus und formt dabei den körperfesten ''Gangpolkegel'' (rot in Abb. 4 und 5). Diese Bewegung der Drehachse wird als [[Präzession]] bezeichnet.
=== Energiebetrachtung ===
 
Multiplikation der Bewegungsgleichung [[#phipp|(*)]] mit <math>\dot\varphi</math> ermöglicht eine Zeitintegration:
Im raumfesten System ist der Drehimpuls
 
:<math>\begin{align}
\vec{L}_s
=&
\mathbf{I}\cdot\vec{\omega}
=I_0\omega_1\hat{g}_1+I_0\omega_2\hat{g}_2+I_3\omega_3\hat{g}_3
=I_0(\vec{\omega}-\omega_3\hat{g}_3)+I_3\omega_3\hat{g}_3
\\=&
I_0\vec{\omega}+(I_3-I_0)\omega_3\hat{g}_3
\end{align}</math>
 
um den Massenmittelpunkt konstant (grün in Abb. 4). An letzterer Zerlegung ist erkennbar, dass der Drehimpuls in der von der Figurenachse und der Winkelgeschwindigkeit <math>\vec{\omega}</math> aufgespannten Ebene liegt. Die Bewegung des kräftefreien symmetrischen Kreisels kann also nur darin bestehen, dass die Figurenachse und die Winkelgeschwindigkeit gemeinsam um die raumfeste Achse drehen, die durch den Drehimpuls definiert ist. Die Bewegung der Figurenachse wird [[Nutation (Physik)|Nutation]] genannt (schwarze Ellipse in Abb. 4 und 5).
 
Das Koordinatensystem kann nun – wie in Abb. 4 – so ausgerichtet werden, dass der Drehimpuls in z-Richtung weist und somit <math>\vec{L}_s=:L\hat{e}_z</math> gilt. Weil sich die [[Rotationsenergie]]


:<math>E_{\rm rot}=\frac{1}{2}\vec{\omega}\cdot\mathbf{I}\cdot\vec{\omega}
:<math>E=
=\frac{1}{2}\vec{\omega}\cdot L\hat{e}_z
\frac{C}{2}{\dot\varphi}^2+\frac{B-A}{2}\mu^2\sin^2(\varphi)
=\frac{1}{2}\omega_z L
+mgs\sin(\varphi)
</math>
</math>


ebenfalls nicht ändert, ist auch die z-Komponente ''ω''<sub>z</sub> der Winkelgeschwindigkeit konstant. Damit bewegt sich die Winkelgeschwindigkeit auch um die raumfeste z-Richtung auf einem Kegel, dem raumfesten ''Rastpolkegel'' (blau in Abb. 4 und 5, dort „raumfester Gangpolkegel“ genannt.) Der Winkel ''β'' zwischen der Figurenachse und dem Drehimpuls sowie die z-Komponente der Winkelgeschwindigkeit können mit der mechanischen Analyse im folgenden Abschnitt ermittelt werden.
Die [[Integrationskonstante]] ''E'' ist die Energie des Pendels im rotierenden System:<ref name="eckelt"/>
 
* der erste Summand trägt die [[Rotationsenergie]] um die 3-Achse bei,
[[Datei:Tr-21.png|mini|Abb. 5: Bewegungsform eines oblaten, kräftefreien Kreisels]]
* der zweite Summand ist das [[Zentrifugalkraft#Zentrifugalpotential|Zentrifugalpotential]] der Präzession und
Die drei Vektoren Drehimpuls, Figurenachse und Winkelgeschwindigkeit ändern ihre relative Position nicht: der Gangpolkegel rollt auf dem Rastpolkegel ab. Beim ''prolaten'' (schlanken) Kreisel ist <math>I_0>I_3</math> und der Gangpolkegel rollt wie in Abb. 4 ''außen'' auf dem Rastpolkegel ab. Beim ''oblaten'' (stämmigen) Kreisel ist <math>I_3>I_0</math> und der Gangpolkegel rollt wie in Abb. 5 ''innen'' auf dem Rastpolkegel ab.
* der dritte Summand steht für die [[Lageenergie]] im Schwerefeld der Erde.
 
Das Abrollen ist sogar [[schlupf]]<nowiki>los</nowiki>, denn die gemeinsame Mantellinie von Rastpol-und Gangpolkegel ist die von der Winkelgeschwindigkeit gestellte momentane Drehachse, die durch den ruhenden Massenmittelpunkt geht (in Abb. 5 anders dargestellt). Die [[Starrer Körper#Allgemeine Bewegungen starrer Körper|eulersche Geschwindigkeitsgleichung]] <math>\dot{\vec{x}}=\dot{\vec{s}}+\vec{\omega}\times (\vec{x}-\vec{s})</math> reduziert sich auf <math>\dot{\vec{x}}=\vec{\omega}\times\vec{x}</math>, wenn der Massenmittelpunkt im Ursprung des Koordinatensystems als Bezugspunkt <math>\vec s</math> gewählt wird. Somit stehen die Partikel des Kreisels auf der Drehachse still (für <math>\vec x\parallel\vec\omega</math>), der Rastpolkegel ruht sowieso, und Schlupf zwischen Gangpol-und Rastpolkegel ist mithin ausgeschlossen.
 
==== Bewegungsfunktion des symmetrischen Kreisels ====
[[Datei:eulerframe.svg|mini|Abb. 6: Das eulersche Basissystem (grün) gibt die Achsen an, um die die Euler-Winkel ''α'', ''β'' und ''γ'' drehen.]]
 
Die Berechnung der Kreiselbewegung im raumfesten Bezugssystem gelingt mit den [[Eulersche Winkel#Standard-x-Konvention (z, x', z")|eulerschen Winkeln]], beispielsweise in der Standard-x-Konvention (z, x', z"), siehe Abb. 6. Bezeichnen die Einheitsvektoren <math>\hat{e}_{x,y,z}</math> die raumfeste [[Standardbasis]] (blau in Abb. 6) und <math>\hat{e}_{X,Y,Z}=\hat{g}_{1,2,3}</math> die mit dem Körper rotierende, bewegte Basis (rot in Abb. 6), dann lauten die mitbewegten Basisvektoren bezüglich der raumfesten Basis:
 
:<math>\begin{align}
\hat{g}_1=&\begin{pmatrix}
\cos(\alpha)\cos(\gamma)-\sin(\alpha)\cos(\beta)\sin(\gamma)\\
\sin(\alpha)\cos(\gamma)+\cos(\alpha)\cos(\beta)\sin(\gamma)\\
\sin(\beta)\sin(\gamma)
\end{pmatrix}
\\
\hat{g}_2=&\begin{pmatrix}
-\cos(\alpha)\sin(\gamma)-\sin(\alpha)\cos(\beta)\cos(\gamma)\\
-\sin(\alpha)\sin(\gamma)+\cos(\alpha)\cos(\beta)\cos(\gamma)\\
\sin(\beta)\cos(\gamma)
\end{pmatrix}
\\
\hat{g}_3=&\begin{pmatrix}
\sin(\alpha)\sin(\beta)\\
-\cos(\alpha)\sin(\beta)\\
\cos(\beta)
\end{pmatrix}
\,.\end{align}</math>
 
Sie finden sich in den Zeilen der Drehmatrix. Wenn, wie im vorherigen Abschnitt, der Drehimpuls in Richtung der z-Achse weist und die Winkelgeschwindigkeit ''ω'' sowie der Winkel ''λ'' vorgegeben werden, dann berechnen sich der Drehimpuls
 
:<math>L=\sqrt{I_3^2\cos^2(\lambda)+I_0^2\sin^2(\lambda)}\,\omega\,,</math>
 
die Winkelgeschwindigkeiten
 
:<math>\begin{align}
\Omega=&\frac{I_3-I_0}{I_0}\omega\cos(\lambda)
\\
\omega_1=&\dot\alpha\sin(\beta)\sin(\gamma)=\omega\sin(\lambda)\cos(\Omega t)
\\
\omega_2=&\dot\alpha\sin(\beta)\cos(\gamma)=\omega\sin(\lambda)\sin(\Omega t)
\\
\omega_3=&\dot\alpha\cos(\beta)+\dot\gamma=\omega\cos(\lambda)
\end{align}</math>
 
und die Winkel
 
:<math>
\alpha=\frac{\pi}{2}+\frac{1}{I_0}\sqrt{I_3^2\cos^2(\lambda)+I_0^2\sin^2(\lambda)}\,\omega t
\,,\quad
\beta=\arctan\left(\frac{I_0}{I_3}\tan(\lambda)\right)
\,,\quad
\gamma=\frac{\pi}{2}-\Omega t
\,.</math>
 
Die Funktion tan ist der [[Tangens und Kotangens|Tangens]] und arctan seine [[Arkusfunktion]]. Die von der z-Achse und der Figurenachse aufgespannte Ebene, die auch den Winkelgeschwindigkeitsvektor enthält, schließt mit der x-z-Ebene den Winkel
:<math>\varphi
=\frac{I_3\cos^2(\lambda)+I_0\sin^2(\lambda)}{\sqrt{I_3^2\cos^2(\lambda)+I_0^2\sin^2(\lambda)}}\,\omega t</math>
 
ein, eine Bewegung, die als Nutation bezeichnet wird.
 
{| class="wikitable mw-collapsible mw-collapsed"
|-
| Beweis&nbsp;
|-
| Der Nachweis gelingt mit dem [[Lagrange-Formalismus]] wie folgt. Bezeichnen die Einheitsvektoren <math>\hat{e}_{x,y,z}</math> die raumfeste [[Standardbasis]] (blau in Abb. 6) und <math>\hat{e}_{X,Y,Z}=\hat{g}_{1,2,3}</math> die mit dem Körper rotierende, bewegte Basis (rot in Abb. 6), dann lauten die Vektoren <math>\hat{u}_{\alpha,\beta,\gamma}</math> des ''eulerschen Bezugssystems'', das die Achsen angibt, um die die Winkel ''α'', ''β'' bzw. ''γ'' drehen (grün in Abb. 6):<br />
<math>\begin{align}
\hat{u}_\alpha
=&\hat{e}_z
\\=&\sin(\beta)\sin(\gamma)\hat{g}_1+\sin(\beta)\cos(\gamma)\hat{g}_2+\cos(\beta)\hat{g}_3
\\
\hat{u}_\beta=&
\cos(\alpha)\hat{e}_x+\sin(\alpha)\hat{e}_y
\\=&
\cos(\gamma)\hat{g}_1-\sin(\gamma)\hat{g}_2
\\
\hat{u}_\gamma=&
\sin(\alpha)\sin(\beta)\hat{e}_x-\cos(\alpha)\sin(\beta)\hat{e}_y+\cos(\beta)\hat{e}_z
\\=&
\hat{g}_3
\end{align}</math><br />
Damit ergibt sich die Winkelgeschwindigkeit im bewegten System zu:<br />
<math>\begin{align}
\vec\omega
=&\dot{\alpha}\hat{u}_\alpha+\dot{\beta}\hat{u}_\beta+\dot{\gamma}\hat{u}_\gamma
\\=&[\underbrace{\dot\alpha\sin(\beta)\sin(\gamma)+\dot\beta\cos(\gamma)}_{\omega_1}]\hat{g}_1+[\underbrace{\dot\alpha\sin(\beta)\cos(\gamma)-\dot\beta\sin(\gamma)}_{\omega_2}]\hat{g}_2
+[\underbrace{\dot\alpha\cos(\beta)+\dot\gamma}_{\omega_3}]\hat{g}_3
\,.\end{align}</math><br />
Der Drehimpuls ist in Abwesenheit äußerer Momente konstant und weise in z-Richtung:<br />
<math>\begin{align}
\vec{L}
=&L\hat{e}_z
=\mathbf{I}\cdot\vec\omega
=I_0\omega_1\hat{g}_1+I_0\omega_2\hat{g}_2+I_3\omega_3\hat{g}_3
\\
L
=&
\vec{L}\cdot\hat{e}_z
=
I_0\omega_1\sin(\beta)\sin(\gamma)+I_0\omega_2\sin(\beta)\cos(\gamma)+I_3\omega_3\cos(\beta)
\\=&
I_0\dot\alpha\sin^2(\beta)+I_3[\dot\alpha\cos(\beta)+\dot\gamma]\cos(\beta)
\end{align}</math><br />
Die Lagrange-Funktion ist hier die kinetische Energie des Kreisels:<br />
<math>
\mathcal{L}:=\frac12\vec{\omega}\cdot\mathbf{I}\cdot\vec{\omega}
=
\frac{I_0}{2}(\omega_1^2+\omega_2^2)+\frac{I_3}{2}\omega_3^2
=
\frac{I_0}{2}[{\dot\alpha}^2\sin^2(\beta)+{\dot{\beta}}^2]+\frac{I_3}{2}[\dot\alpha\cos(\beta)+\dot\gamma]^2
\,.</math><br />
Dem Lagrange-Formalismus zufolge sind die Winkel ''α'' und ''γ'' ''zyklisch'' und ihre '' [[Generalisierter Impuls|konjugierten Impulse]]'' konstant:<br />
<math>\begin{align}
p_\alpha:=&\frac{\partial\mathcal{L}}{\partial\dot{\alpha}}
=
I_0\dot\alpha\sin^2(\beta)+I_3[\dot\alpha\cos(\beta)+\dot\gamma]\cos(\beta)
=
L
=\text{const.}
\\[1ex]
p_\gamma:=&\frac{\partial\mathcal{L}}{\partial\dot{\gamma}}
=I_3[\dot\alpha\cos(\beta)+\dot\gamma]
=I_3\omega_3
=\vec{L}\cdot\hat{g}_3
=L\cos(\beta)
=\text{const.}
\end{align}</math><br />
Die erste Gleichung bestätigt die Erhaltung des Drehimpulses und die zweite zeigt, dass die Winkelgeschwindigkeit ''ω''<sub>3</sub> um die Figurenachse und der Winkel ''β'' zwischen der Figurenachse und der z-Richtung konstant sind.<br />
Die dritte Bewegungsgleichung resultiert aus der Lagrange-Funktion für ''β'':<br />
<math>\begin{align}
\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial\mathcal{L}}{\partial\dot\beta}
=&
\frac{\partial\mathcal{L}}{\partial\beta}
\\
\rightarrow
I_0\ddot\beta
=
0
=&
I_0{\dot\alpha}^2\sin(\beta)\cos(\beta)-I_3[\dot\alpha\cos(\beta)+\dot\gamma]\dot\alpha\sin(\beta)
=
[I_0\dot\alpha\cos(\beta)-I_3\omega_3]\dot\alpha\sin(\beta)
\\
\rightarrow
\dot\alpha
=&
\frac{I_3\omega_3}{I_0\cos(\beta)}=\text{const.}
\end{align}</math><br />
Für den Drehimpuls bedeutet das:<br />
<math>L
=
I_0\dot\alpha\sin^2(\beta)+I_3\omega_3\cos(\beta)
=
I_0\dot\alpha\sin^2(\beta)+I_0\dot\alpha\cos^2(\beta)
=
I_0\dot\alpha
=
\frac{I_3\omega_3}{\cos(\beta)}
\,.</math><br />
Aus <math>\omega_3=\dot\alpha\cos(\beta)+\dot\gamma</math> folgt weiter<br />
<math>\dot\gamma
=\omega_3-\dot\alpha\cos(\beta)
=\omega_3-\frac{I_3\omega_3}{I_0\cos(\beta)}\cos(\beta)
=\frac{I_0-I_3}{I_0}\omega_3
=-\Omega
=\text{const.}
</math><br />
Im eulerschen Bezugssystem ist <math>\vec\omega=\dot\alpha\hat{e}_z+\dot\gamma\hat{g}_3</math> wegen <math>\dot\beta=0</math>. Die Winkelgeschwindigkeit um die z-Achse berechnet sich damit zu<br />
<math>\omega_z
:=\vec{\omega}\cdot\hat{e}_z
=\dot\alpha+\dot\gamma(\hat{g}_3\cdot\hat{e}_z)
=\dot\alpha+\dot\gamma\cos(\beta)
=\frac{L}{I_0}+\frac{I_0-I_3}{I_0}\frac{I_3}{L}\omega_3^2
\,.</math>
|-
! Anfangsbedingungen
|-
| Zur Zeit ''t''=0 ist <math>\omega_3=\vec{\omega}\cdot\hat{g}_3=\omega\cos(\lambda)</math> und diesen Wert behält ''ω''<sub>3</sub>. Der Winkel ''β'' kann nun als Funktion des Winkels ''λ'' ausgedrückt werden:<br />
<math>\begin{align}
\omega\cos(\lambda)
=&
\omega_3
=
\dot\alpha\cos(\beta)+\dot\gamma
=
\dot\alpha\cos(\beta)-\Omega
\\
\omega\sin(\lambda)
=&
\omega_\bot
=
\sqrt{\omega_1^2+\omega_2^2}
=
\dot\alpha\sin(\beta)
\\
\rightarrow
\cot(\lambda)
=&
\cot(\beta)-\frac{\Omega}{\dot\alpha\sin(\beta)}
=
\cot(\beta)+\frac{I_0-I_3}{I_0}\omega_3\frac{I_0\cos(\beta)}{I_3\omega_3\sin(\beta)}
=
\cot(\beta)+\frac{I_0-I_3}{I_3}\cot(\beta)
\\
\rightarrow
\tan(\beta)=&\frac{I_0}{I_3}\tan(\lambda)
\,.\end{align}</math><br />
Der [[Tangens und Kotangens|Kotangens]] cot ist der Kehrwert des Tangens. Wegen <math>\cos x=(1+\tan^2 x)^{-1/2}</math> und <math>\tan(\beta)=\tfrac{I_0}{I_3}\tan(\lambda)</math> folgt für den Drehimpuls:<br />
<math>L
=
\frac{I_3\omega_3}{\cos(\beta)}
=
\frac{I_3\omega\cos(\lambda)}{\cos(\beta)}
=
\sqrt{I_3^2\cos^2(\lambda)+I_0^2\sin^2(\lambda)}\,\omega
\,.</math><br />
Die Vorgaben<br />
<math>\begin{align}
\omega_1(t=0)
=&\dot\alpha\sin(\beta)\sin(\gamma)
=\omega\sin(\lambda)\sin(\gamma)
\,\stackrel{\displaystyle !}{=}\,\omega\sin(\lambda)
\\
\omega_2(t=0)
=&\dot\alpha\sin(\beta)\cos(\gamma)
=\omega\sin(\lambda)\cos(\gamma)
\,\stackrel{\displaystyle !}{=}\,0
\end{align}</math><br />
können mit dem Anfangswert des Winkels ''γ'' von <math>\tfrac{\pi}{2}</math> erfüllt werden, sodass <math>\gamma=\tfrac{\pi}{2}-\Omega t</math>. Die Winkelgeschwindigkeit lautet zur Zeit ''t''=0:<br />
<math>\vec{\omega}
=\omega\sin(\lambda)\hat{g}_1+\omega\cos(\lambda)\hat{g}_3
=\omega\begin{pmatrix}
\sin(\alpha)\sin(\beta-\lambda)\\
-\cos(\alpha)\sin(\beta-\lambda)\\
\cos(\beta-\lambda)
\end{pmatrix}
\,.</math><br />
Damit diese in der x-z-Ebene liegt, wird der Anfangswert von ''α'' auf <math>\tfrac{\pi}{2}</math> gesetzt, sodass sich<br />
<math>\alpha
=\frac{\pi}{2}+\dot\alpha t
=\frac{\pi}{2}+\frac{L}{I_0}t
=\frac{\pi}{2}+\frac{1}{I_0}\sqrt{I_3^2\cos^2(\lambda)+I_0^2\sin^2(\lambda)}\,\omega t
</math><br />
ergibt. Wenn der Drehwinkel der Figurenachse um die z-Achse mit ''φ'' bezeichnet wird und zu Beginn den Wert null hat, dann folgt:<br />
<math>\varphi:=\omega_z t
=\left[\frac{L}{I_0}+\frac{I_0-I_3}{I_0}\frac{I_3}{L}\cos^2(\lambda)\omega^2\right]t
=\frac{I_3\cos^2(\lambda)+I_0\sin^2(\lambda)}{\sqrt{I_3^2\cos^2(\lambda)+I_0^2\sin^2(\lambda)}}\,\omega t
\,.</math>
|}
 
=== Kräftefreier unsymmetrischer Kreisel ===
Unsymmetrische Kreisel besitzen [[per definitionem]] drei verschiedene Hauptträgheitsmomente. Dreht sich ein solcher Kreisel um die 3-Achse, dann kann diese Bewegung instabil oder stabil sein. Im ersteren Fall nehmen kleine Störungen [[Exponentialfunktion|exponentiell]] zu und der Kreisel beginnt zu torkeln, was im nächsten Abschnitt begründet wird. Im stabilen Fall bilden sich periodische Bewegungsformen des zweiten Abschnitts aus. Über den Spezialfall der Bewegung auf der Separatrix, die im Abschnitt [[#Allgemeine Eigenschaften der Bewegung krätefrei rotierender Kreisel]] definiert wurde, wird am Schluss informiert.
 
==== Stabilität der Bewegung unsymmetrischer Kreisel ====
[[Datei:Dzhanibekov effect.ogv|mini|Dschanibekow-Effekt: in der Schwerelosigkeit gefilmte Bewegung eines Bauteils um seine instabile Hauptträgheitsachse. Es sei betont, dass der Drehimpuls des Bauteils dabei erhalten bleibt.]]
 
Die Hauptachsen mit dem größten oder dem kleinsten Hauptträgheitsmoment sind stabile Drehachsen. Dies ist spätestens seit 1851 bekannt<ref>[[Louis Poinsot]]: ''Théorie nouvelle de la rotation des corps.'' Bachelier, Paris 1834/1851.</ref> und mit einem rotierend in die Höhe geworfenen [[Tischtennisschläger]] auch leicht zu demonstrieren. Im Englischen ist die Aussage entsprechend als „Satz vom Tennisschläger“ ''(tennis racket theorem)''<ref>''[[:en:Tennis racket theorem|tennis racket theorem]]'' in der englischsprachigen Wikipedia</ref> geläufig. Nachdem der sowjetische Kosmonaut [[Wladimir Alexandrowitsch Dschanibekow|Wladimir Dschanibekow]] während eines Raumfluges 1985 die Bewegung eines Bauteils um seine instabile Hauptträgheitsachse beobachtet hat, wurde der Sachverhalt genauer untersucht<ref>Mark S. Ashbaugh, Carmen C. Chicone, Richard H. Cushman: ''The twisting tennis racket.'' In: ''Journal of Dynamics and Differential Equations'', 3, 1, 1991, S. 67–85.</ref> und wird seitdem gelegentlich „[[Dschanibekow-Effekt]]“ genannt.


Um die Stabilität der Drehachsen zu prüfen, soll der Kreisel zunächst vor allem um die 3-Achse rotieren: <math>\omega_3\ne 0</math> und <math>|\omega_{1,2}|\ll\sqrt{|\dot\omega_3|}</math>. Nun lauten die Kreiselgleichungen
Die Energie und ihre Ableitungen (·)' nach ''φ'' ergeben sich mit der Abkürzung <math>z:=\tfrac{mgs}{(A-B)\mu^2}</math> zu


:<math>\begin{align}
:<math>\begin{align}
0=&\dot{\omega}_1-\frac{I_2-I_3}{I_1}\omega_2\omega_3
E=&\frac{C}{2}{\dot\varphi}^2
+(B-A)\mu^2\bigg(\frac{\sin^2(\varphi)}{2}-z\sin(\varphi)\bigg)
\\
\\
0=&\dot{\omega}_2-\frac{I_3-I_1}{I_2}\omega_3\omega_1
E'=&(B-A)\mu^2[\sin(\varphi)-z]\cos(\varphi)
\\
\\
0=&\dot{\omega}_3-\frac{I_1-I_2}{I_3}\omega_1\omega_2\approx\dot{\omega}_3
E''=&(B-A)\mu^2[1+z \sin(\varphi)-2\sin^2(\varphi)]
\end{align}</math>
\end{align}</math>


Analog zur [[#Betrachtung im rotierenden Bezugssystem]] entsteht durch Ableitungen nach der Zeit und mit der näherungsweisen Konstanz der Winkelgeschwindigkeit ''ω''<sub>3</sub>:
Beim gestreckten Kreisel ist ''B&nbsp;>&nbsp;A'' und ''z''&nbsp;<&nbsp;0 und beim abgeplattenten Kreisel ist ''B&nbsp;<&nbsp;A'' sowie ''z''&nbsp;>&nbsp;0. Stabilität liegt in einem Energieminimum vor, wo ''E<nowiki>'</nowiki>''&nbsp;=&nbsp;0 und ''E''"&nbsp;>&nbsp;0 ist. Die Energie ist in [[#Gleichgewichtslagen|Gleichgewichtslagen]] stationär: bei sin(''φ'')&nbsp;=&nbsp;''z'' oder cos(''φ'')&nbsp;=&nbsp;0, wo sin(''φ'')&nbsp;=&nbsp;-1 oder sin(''φ'')&nbsp;=&nbsp;+1 ist:
;Gleichgewichtslage mit sin(''φ'')&nbsp;=&nbsp;''z''
: Hier ist ''E"&nbsp;=&nbsp;(A-B)μ²(z²-1)''. Diese Bewegung ist beim gestreckten Kreisel stabil, wenn ''z''<sup>&nbsp;2</sup>&nbsp;<&nbsp;1, also immer, und beim abgeplatteten, wenn ''z''<sup>&nbsp;2</sup>&nbsp;>&nbsp;1, also nie.
;Hängendes Pendel sin(''φ'')&nbsp;=&nbsp;-1
: Hier ist ''E"&nbsp;=&nbsp;(A-B)μ²(1+z)''. Der untere Totpunkt ist beim abgeplatteten Kreisel stabil, wenn ''z''&nbsp;>&nbsp;-1, also immer, und beim gestreckten, wenn ''z''&nbsp;<&nbsp;-1, also |''μ''|&nbsp;<&nbsp;''μ''<sub>c</sub>. Bei zunehmendem ''μ'' durchläuft das gestreckte Pendel bei ''μ''&nbsp;=&nbsp;''μ''<sub>c</sub> eine subkritische [[Pitchfork-Bifurkation]]<ref name="eckelt" />, wo die stabile Lage am unteren Totpunkt instabil wird und zwei stabile Gleichgewichtslagen mit sin(''φ'')&nbsp;=&nbsp;''z'' entstehen. Im Gegensatz dazu ist der [[Lagrange-Kreisel#Lotrecht hängender Kreisel|lotrecht hängende Lagrange-Kreisel]] immer stabil<ref>Grammel (1920), S. 111.</ref>, siehe dort.
;Aufrechtes Pendel sin(''φ'')&nbsp;=&nbsp;+1
: Hier ist ''E"&nbsp;=&nbsp;(A-B)μ²(1-z)''. Der obere Totpunkt ist beim gestreckten Kreisel stabil, wenn ''z''&nbsp;>&nbsp;1, also nie, und beim abgeplatteten, wenn ''z''&nbsp;<&nbsp;1 oder |''μ''|&nbsp;>&nbsp;''μ''<sub>c</sub>. Bei zunehmendem ''μ'' durchläuft das abgeplattete Pendel bei ''μ''&nbsp;=&nbsp;''μ''<sub>c</sub> eine superkritische [[Pitchfork-Bifurkation]], wo die instabile Lage am oberen Totpunkt stabil wird und zwei neue instabile Gleichgewichtslagen mit sin(''φ'')&nbsp;=&nbsp;''z'' entstehen.


:<math>\begin{align}
=== Schwingungen ===
0
Die Gleichung [[#phipp|(*)]] kann um [[#Gleichgewichtslagen|Gleichgewichtslagen]]''φ''<sub>0</sub>, wo ''z''&nbsp;=&nbsp;sin(''φ''<sub>0</sub>) ist, linearisiert werden. Dazu wird ''φ''&nbsp;=&nbsp;''φ''<sub>0</sub>+''δ'' mit konstantem ''φ''<sub>0</sub> und kleiner Abweichung ''δ'' angenommen. Die Drehbeschleunigung
=&\ddot{\omega}_1-\frac{I_2-I_3}{I_1}\omega_3\dot{\omega}_2
=\ddot{\omega}_1-\frac{I_2-I_3}{I_1}\frac{I_3-I_1}{I_2}\omega_3^2\omega_1
=\ddot{\omega}_1+k\omega_1
\\
0
=&\ddot{\omega}_2-\frac{I_3-I_1}{I_2}\omega_3\dot{\omega}_1
=\ddot{\omega}_2-\frac{I_3-I_1}{I_2}\frac{I_2-I_3}{I_1}\omega_3^2\omega_2
=\ddot{\omega}_2+k\omega_2
\\
&\text{mit}\quad
k:=\frac{I_1-I_3}{I_2}\frac{I_2-I_3}{I_1}\omega_3^2
\end{align}</math>
 
Falls ''k'' negativ ist, kommt es zu [[Positive Rückkopplung|positiver Rückkopplung]] der Winkelgeschwindigkeiten und damit zum Verlassen der Rotation um die 3-Achse hin zu einem Torkeln. Falls ''k'' positiv ist, ergeben sich periodische Bewegungsformen. Dafür müssen die Hauptträgheitsmomente ''I''<sub>1,2</sub> entweder beide größer oder beide kleiner als das dritte Hauptträgheitsmoment ''I''<sub>3</sub> sein, woraus die obige Aussage über die Stabilität der Achsen folgt.
 
==== Bewegungsfunktion des unsymmetrischen Kreisels ====
[[Datei:JacobiEllipticFunctionsk095.png|mini|Abb. 7: Zeitverläufe der Jacobi’schen elliptischen Funktionen sn, cn und dn bei k=0,95]]
Die Hauptträgheitsmomente seien derart nummeriert, dass ''I''<sub>1</sub>< ''I''<sub>2</sub>< ''I''<sub>3</sub> gilt. Dann können die Kreiselgleichungen im kräftefreien Fall mit den [[Jacobische elliptische Funktion|Jacobi’schen elliptischen Funktionen]] sn, cn und dn erfüllt werden<ref name="wipf">{{Internetquelle |autor=Andreas Wipf |hrsg=Universität Jena |url=http://homepages.physik.uni-muenchen.de/~michael.haack/Wipf_Mechanik.pdf |format=PDF |sprache=deutsch |titel=Theoretische Mechanik |titelerg=Vorlesungs-Skriptum |seiten=153 bis 160 |datum=2003 |zugriff=2016-07-02}}</ref>. Aus der Rotationsenergie und dem Betragsquadrat des Drehimpulses
:<math>E_\text{rot}:=\frac12\vec\omega\cdot\mathbf{I}\cdot\vec\omega
=\frac12(I_1\omega_1^2+I_2\omega_2^2+I_3\omega_3^2)
\,,\quad
L^2:=\vec{L}\cdot\vec{L}=I_1^2\omega_1^2+I_2^2\omega_2^2+I_3^2\omega_3^2
\,.</math>
 
ergeben sich die Winkelgeschwindigkeiten
 
:<math>\begin{align}
\omega_1=&A_1\operatorname{cn}(at;k)
\\
\omega_2=&A_2\operatorname{sn}(at;k)
\\
\omega_3=&A_3\operatorname{dn}(at;k)
\end{align}</math>


mit den Amplituden
:<math>
:<math>
A_1=\sqrt{\frac{2I_3E_\text{rot}-L^2}{I_1(I_3-I_1)}}
C\ddot\varphi=C\ddot\delta
\,,\quad
=(A-B)\mu^2\sin(\varphi_0+\delta)\cos(\varphi_0+\delta)
A_2=\sqrt{\frac{2I_3E_\text{rot}-L^2}{I_2(I_3-I_2)}}
-mgs\cos(\varphi_0+\delta)
\,,\quad
A_3=\sqrt{\frac{L^2-2I_1E_\text{rot}}{I_3(I_3-I_1)}}
\,,</math>
 
der Frequenz und dem ''elliptischen Modul''
:<math>a=\sqrt{\frac{I_3-I_2}{I_1I_2I_3}(L^2-2I_1E_\text{rot})}
\,,\quad
k=\sqrt{\frac{I_2-I_1}{I_3-I_2}\,\frac{2I_3E_\text{rot}-L^2}{L^2-2I_1E_\text{rot}}}
\,.</math>
 
Es zeigt sich
 
:<math>\begin{align}
2I_3E_\text{rot}-L^2
=&
I_1(I_3-I_1)\omega_1^2+I_2(I_3-I_2)\omega_2^2 > 0
\\
L^2-2I_1E_\text{rot}
=&
I_2(I_2-I_1)\omega_2^2+I_3(I_3-I_1)\omega_3^2 > 0
\,,\end{align}</math>
 
sodass die vorgenannten Konstanten reell sind. Die Funktionen sn und cn sind periodisch mit der Periode 4''K'' und dn mit der Periode 2''K'', siehe Abb. 7. Dabei ist ''K'' das [[Elliptisches Integral#Vollständige elliptische Integrale|vollständige elliptische Integral erster Art]]:
 
:<math>K:=\int_0^{\frac{\pi}{2}}\frac{\mathrm{d}\theta}{\sqrt{1-k^2\sin^2\theta}}\,.</math>
 
Damit ist die Winkelgeschwindigkeit periodisch mit der Periodenlänge <math>T=\tfrac{4K}{a}</math>. Nach dieser Zeit ist die Winkelgeschwindigkeit wieder in ihren Ausgangszustand zurückgekehrt: <math>\vec\omega(T)=\vec\omega(0)\,.</math>
 
Allerdings gilt das nicht für den Kreisel als Ganzem: Dieser kehrt im Allgemeinen nicht in eine Anfangslage zurück.<ref name="wipf" /> Die eulerschen Winkel – siehe [[#Bewegungsfunktion des symmetrischen Kreisels]] – ergeben sich zu
 
:<math>\begin{align}
\dot\alpha
=&
L\frac{I_3-I_2+(I_2-I_1)\operatorname{sn}^2(at;k)
}{
I_1(I_3-I_2)+I_3(I_2-I_1)\operatorname{sn}^2(at;k)
}
\\
\cos(\beta)
=&
\sqrt{\frac{I_3}{I_3-I_1}\frac{L^2-2I_1E_\text{rot}}{L^2}}\operatorname{dn}(at;k)
\\
\tan(\gamma)
=&
\sqrt{\frac{I_1(I_3-I_2)}{I_2(I_3-I_1)}}\frac{\operatorname{cn}(at;k)}{\operatorname{sn}(at;k)}
\end{align}</math>
 
Die Formeln bleiben gültig, wenn die Hauptträgheitsmomente die umgekehrte Reihenfolge ''I''<sub>1</sub> > ''I''<sub>2</sub> > ''I''<sub>3</sub> aufweisen. Allerdings kehren die Differenzen
 
:<math>\begin{align}
2I_3E_\text{rot}-L^2
=&
I_1(I_3-I_1)\omega_1^2+I_2(I_3-I_2)\omega_2^2 < 0
\\
L^2-2I_1E_\text{rot}
=&
I_2(I_2-I_1)\omega_2^2+I_3(I_3-I_1)\omega_3^2 < 0
\end{align}</math>
 
dann ihr Vorzeichen um. Anders als beim kräftefreien symmetrischen Kreisel sind die Winkelgeschwindigkeiten <math>\omega_3,\,\dot\alpha,\,\dot\gamma</math> und der Winkel ''β'' zwischen dem Drehimpuls und der 3-Achse ''nicht'' konstant. Im Spezialfall ''I''<sub>1</sub>=''I''<sub>2</sub> ist ''A''<sub>1</sub>=''A''<sub>2</sub> und ''k''=0, sodass die elliptischen Funktionen sn und cn in die harmonischen Funktionen sin bzw. cos übergehen und dn≡1 ist. Dann geht die hiesige Lösung in die des symmetrischen Kreisels über.
 
{| class="wikitable mw-collapsible mw-collapsed"
|-
| Beweis&nbsp;
|-
| Zunächst wird gezeigt, dass die Winkelgeschwindigkeiten den eulerschen Kreiselgleichungen genügen. Die Jacobi’schen elliptischen Funktionen erfüllen die Differentialgleichungen<br />
<math>\begin{align}
\frac{\mathrm{d}}{\mathrm{d}z}\operatorname{sn}(z;k)=&\operatorname{cn}(z;k)\operatorname{dn}(z;k)
\\
\frac{\mathrm{d}}{\mathrm{d}z}\operatorname{cn}(z;k)=&-\operatorname{sn}(z;k)\operatorname{dn}(z;k)
\\
\frac{\mathrm{d}}{\mathrm{d}z}\operatorname{dn}(z;k)=&-k^2\operatorname{sn}(z;k)\operatorname{cn}(z;k)
\end{align}</math><br />
Mit <math>z=at</math> und <math>\dot z=a</math> ergibt sich daraus im Einklang mit den Kreiselgleichungen:<br />
<math>\begin{align}
\dot{\omega}_1=&A_1\frac{\mathrm{d}}{\mathrm{d}t}\operatorname{cn}(at;k)
=A_1\frac{\mathrm{d}}{\mathrm{d}z}\operatorname{cn}(z;k)\dot z
=-A_1a\operatorname{sn}(at;k)\operatorname{dn}(at;k)
=-\frac{A_1a}{A_2A_3}\omega_2\omega_3
=
\frac{I_2-I_3}{I_1}\omega_2\omega_3
\\
\dot{\omega}_2=&
A_2\frac{\mathrm{d}}{\mathrm{d}t}\operatorname{sn}(at;k)
=
A_2\frac{\mathrm{d}}{\mathrm{d}z}\operatorname{sn}(z;k)\dot{z}
=
A_2a\operatorname{cn}(at;k)\operatorname{dn}(at;k)
=
\frac{A_2a}{A_1A_3}\omega_1\omega_3
=
\frac{I_3-I_1}{I_2}\omega_1\omega_3
\\
\dot{\omega}_3
=&
A_3\frac{\mathrm{d}}{\mathrm{d}t}\operatorname{dn}(at;k)
=
A_3\frac{\mathrm{d}}{\mathrm{d}z}\operatorname{dn}(z;k)\dot{z}
=
-A_3ak^2\operatorname{sn}(at;k)\operatorname{cn}(at;k)
=
-\frac{A_3ak^2}{A_1A_2}\omega_1\omega_2
=
\frac{I_1-I_2}{I_3}\omega_1\omega_2
\,.\end{align}</math><br />
Vergleich der Komponenten des Drehimpulses in euler-Winkeln (siehe [[#Betrachtung im rotierenden Bezugssystem]] beim symmetrischen Kreisel) liefert im mitbewegten System <math>\hat{g}_{1,2,3}</math>:<br />
<math>\begin{align}
\vec L
=&
L\hat{e}_z
=
L
\begin{pmatrix}
\sin(\beta)\sin(\gamma)
\\
\sin(\beta)\cos(\gamma)
\\
\cos(\beta)
\end{pmatrix}_{\hat{g}_i}
=
\begin{pmatrix}L_1\\L_2\\L_3\end{pmatrix}_{\hat{g}_i}
=
\mathbf{I}\cdot\vec\omega
=
\begin{pmatrix}I_1\omega_1\\ I_2\omega_2\\ I_3\omega_3\end{pmatrix}_{\hat{g}_i}
=
\begin{pmatrix}
I_1A_1\operatorname{cn}(at;k)
\\
I_2A_2\operatorname{sn}(at;k)
\\
I_3A_3\operatorname{dn}(at;k)
\end{pmatrix}_{\hat{g}_i}
\\
\rightarrow\cos(\beta)=&\frac{L_3}{L}
=\frac{I_3A_3}{L}\operatorname{dn}(at;k)
=\sqrt{\frac{I_3}{I_3-I_1}\frac{L^2-2I_1E_\text{rot}}{L^2}}\operatorname{dn}(at;k)
\\
\tan(\gamma)=&\frac{L_1}{L_2}
=\frac{I_1A_1\operatorname{cn}(at;k)}{I_2A_2\operatorname{sn}(at;k)}
=\sqrt{\frac{I_1(I_3-I_2)}{I_2(I_3-I_1)}}\frac{\operatorname{cn}(at;k)}{\operatorname{sn}(at;k)}
\end{align}</math><br />
Der Winkel ''α'' bestimmt sich mit <math>L_1^2+L_2^2=I_1^2\omega_1^2+I_2^2\omega_2^2=L^2\sin^2(\beta)</math> und cn²=1-sn² aus
:<math>\begin{align}
\vec\omega
=&
\begin{pmatrix}\omega_1 \\ \omega_2 \\ \omega_3\end{pmatrix}_{\hat{g}_i}
=
\begin{pmatrix}
\dot\alpha\sin(\beta)\sin(\gamma)+\dot\beta\cos(\gamma)
\\
\dot\alpha\sin(\beta)\cos(\gamma)-\dot\beta\sin(\gamma)
\\
\dot\alpha\cos(\beta)+\dot\gamma
\end{pmatrix}_{\hat{g}_i}
\\
\rightarrow\dot\alpha
=&
\frac{\omega_1\sin(\gamma)+\omega_2\cos(\gamma)}{\sin(\beta)}
=
L\frac{\omega_1\overbrace{L\sin(\beta)\sin(\gamma)}^{L_1=I_1\omega_1}
+\omega_2\overbrace{L\sin(\beta)\cos(\gamma)}^{L_2=I_2\omega_2}}{L^2\sin^2(\beta)}
=
L\frac{I_1\omega_1^2+I_2\omega_2^2}{I_1^2\omega_1^2+I_2^2\omega_2^2}
\\=&
L\frac{I_1A_1^2\operatorname{cn}^2(at;k)+I_2A_2^2\operatorname{sn}^2(at;k)
}{
I_1^2A_1^2\operatorname{cn}^2(at;k)+I_2^2A_2^2\operatorname{sn}^2(at;k)
}
=
L\frac{I_3-I_2+(I_2-I_1)\operatorname{sn}^2(at;k)
}{
I_1(I_3-I_2)+I_3(I_2-I_1)\operatorname{sn}^2(at;k)
}
\,.\end{align}</math>
|}
 
==== Bewegung auf der Separatrix ====
[[Datei:separatrixLoxodrome.png|mini|Abb. 8: Weg eines Punktes auf der 2-Achse (rot) um die Drehimpulsachse (senkrechte Linie) entlang einer Loxodrome]]
Auf der Separatrix ist <math>2I_2 E_{\rm rot}=L^2</math> und die Bewegung aperiodisch, weil die Winkelgeschwindigkeit keinen Zustand ein zweites Mal einnimmt. Die Bewegung des Kreisels ist hier dadurch gekennzeichnet, dass die von der 2-Achse und dem Drehimpuls aufgespannte Ebene mit konstanter Winkelgeschwindigkeit ''L''/''I''<sub>2</sub> um die Drehimpulsachse kreist und der Endpunkt der 2-Achse sich auf einer [[Loxodrome]] mit dem Richtungswinkel
 
:<math>\cos\eta=\sqrt{\frac{(I_3-I_2)(I_2-I_1)}{I_2 (I_1+I_3-I_2)}}</math>
 
der durch den Drehimpuls definierten Achse nähert, siehe Abb. 8. Die Formeln des vorangegangenen Abschnitts sind hier zwar gültig, aber weil der elliptische Modul den Extremwert
 
:<math>k=\sqrt{\frac{I_2-I_1}{I_3-I_2}\,\frac{2I_3E_\text{rot}-L^2}{L^2-2I_1E_\text{rot}}}
=\sqrt{\frac{I_2-I_1}{I_3-I_2}\,\frac{2I_3E_\text{rot}-2I_2 E_{\rm rot}}{2I_2 E_{\rm rot}-2I_1E_\text{rot}}}
=1
</math>
</math>


annimmt, gehen die elliptischen Funktionen in die aperiodischen [[Hyperbelfunktion]]en über:
entwickelt sich mit den [[Formelsammlung Trigonometrie #Additionstheoreme|Additionstheoremen]] und sin(''δ'')&nbsp;≈&nbsp;''δ'', cos(''δ'')&nbsp;≈&nbsp;1 zur [[Schwingungsgleichung]]
 
:<math>\operatorname{cn}(at;1)=\operatorname{dn}(at;1)=\frac{1}{\cosh(at)}</math> und <math>\operatorname{sn}(at;1)=\tanh(at).</math>
 
Die Frequenz und die Winkelgeschwindigkeiten des vorangegangenen Abschnitts spezialisieren sich damit zu:
 
:<math>\begin{align}
a=&\sqrt{\frac{I_3-I_2}{I_1I_2I_3}(L^2-2I_1E_\text{rot})}
=\sqrt{\frac{(I_3-I_2)(I_2-I_1)}{I_1I_2^2I_3}}L
\\
\omega_1=&
\sqrt{\frac{2I_3E_\text{rot}-L^2}{I_1(I_3-I_1)}}\operatorname{cn}(at;k)
=\sqrt{\frac{I_3-I_2}{I_1I_2(I_3-I_1)}}\frac{L}{\cosh(at)}
\\
\omega_2=&\sqrt{\frac{2I_3E_\text{rot}-L^2}{I_2(I_3-I_2)}}\operatorname{sn}(at;k)
=\frac{L}{I_2}\tanh(at)
\\
\omega_3=&\sqrt{\frac{L^2-2I_1E_\text{rot}}{I_3(I_3-I_1)}}\operatorname{dn}(at;k)
=\sqrt{\frac{I_2-I_1}{I_2I_3(I_3-I_1)}}\frac{L}{\cosh(at)}
\end{align}</math>
 
Mit fortschreitender Zeit gehen ''ω''<sub>1</sub> und ''ω''<sub>3</sub> gegen null und ''ω''<sub>2</sub> gegen ''L''/''I''<sub>2</sub>. Die Bewegung kommt einer Drehung um die 2-Achse beliebig nah ohne diesen Zustand jemals zu erreichen. In der Realität wird diese Bewegungsform kaum auftreten, denn bei der kleinsten Abweichung vom Idealfall <math>2I_2 E_{\rm rot}=L^2</math> ist ''k''≠1 und die Winkelgeschwindigkeiten werden zu den periodischen des vorangegangenen Abschnitts. Eine Bewegung nahe der Separatrix zeigt der [[Dschanibekow-Effekt]].
 
[[Datei:eulerwinkelzxy.png|mini|Abb. 9: Verwendetes Basissystem <math>\hat{h}_{1,2,3}</math> und Meridian <math>\hat m</math>]]
Für die Berechnung der Bewegung wird, anders als im vorigen Abschnitt, der Ansatz <math>\hat{h}_{1,2,3}=\hat{e}_{Y,Z,X}</math> für das lokale Basissystem benutzt, siehe Abb. 9 und vgl. Abb. 6.
 
Die eulerschen Winkel – siehe [[#Bewegungsfunktion des symmetrischen Kreisels]] – ergeben sich bei einem Drehimpuls in z-Richtung und einem Start mit ''ω''<sub>2</sub>=0 zu
 
:<math>\begin{align}
\dot\alpha=&\frac{L}{I_2}
\\
\cos(\beta)=&\tanh(at)
\\
\tan(\gamma)=&\sqrt{\frac{I_3(I_2-I_1)}{I_1(I_3-I_2)}}
\,.\end{align}</math>
 
Die von der 2-Achse und dem Drehimpuls aufgespannte Ebene kreist mit konstanter Winkelgeschwindigkeit ''L''/''I''<sub>2</sub> um die Drehimpulsachse und der Winkel ''β'' geht mit fortschreitender Zeit gegen null.
 
{| class="wikitable mw-collapsible mw-collapsed"
|-
| Beweis&nbsp;
|-
| Denn im Basissystem<br />
<math>\begin{align}
\hat{h}_1=&\hat{e}_Y=\hat{g}_2=\begin{pmatrix}
-\cos(\alpha)\sin(\gamma)-\sin(\alpha)\cos(\beta)\cos(\gamma)\\
-\sin(\alpha)\sin(\gamma)+\cos(\alpha)\cos(\beta)\cos(\gamma)\\
\sin(\beta)\cos(\gamma)
\end{pmatrix}
\\
\hat{h}_2=&\hat{e}_Z=\hat{g}_3=\begin{pmatrix}
\sin(\alpha)\sin(\beta)\\
-\cos(\alpha)\sin(\beta)\\
\cos(\beta)
\end{pmatrix}
\\
\hat{h}_3=&\hat{e}_X=\hat{g}_1=\begin{pmatrix}
\cos(\alpha)\cos(\gamma)-\sin(\alpha)\cos(\beta)\sin(\gamma)\\
\sin(\alpha)\cos(\gamma)+\cos(\alpha)\cos(\beta)\sin(\gamma)\\
\sin(\beta)\sin(\gamma)
\end{pmatrix}
\end{align}</math><br />
ergibt sich:<br />
<math>\begin{align}
\vec L
=&
L\hat{e}_z
=
L
\begin{pmatrix}
\sin(\beta)\cos(\gamma)
\\
\cos(\beta)
\\
\sin(\beta)\sin(\gamma)
\end{pmatrix}_{\hat{h}_i}
=
\begin{pmatrix}L_1\\L_2\\L_3\end{pmatrix}_{\hat{h}_i}
=
\mathbf{I}\cdot\vec\omega
=
\begin{pmatrix}I_1\omega_1\\ I_2\omega_2\\ I_3\omega_3\end{pmatrix}_{\hat{h}_i}
\\
\rightarrow\cos(\beta)=&\frac{L_2}{L}
=\frac{I_2\omega_2}{L}
=\frac{I_2}{L}\frac{L}{I_2}\tanh(at)
=\tanh(at)
\\
\tan(\gamma)=&\frac{L_3}{L_1}
=\frac{I_3}{I_1}\frac{\omega_3}{\omega_1}
=\frac{I_3}{I_1}\frac{\sqrt{\frac{I_2-I_1}{I_2I_3(I_3-I_1)}}\frac{L}{\cosh(at)}}
{\sqrt{\frac{I_3-I_2}{I_1I_2(I_3-I_1)}}\frac{L}{\cosh(at)}}
=\sqrt{\frac{I_3(I_2-I_1)}{I_1(I_3-I_2)}}
\end{align}</math><br />
Die Komponenten der Winkelgeschwindigkeit werden mit dem neuen Basissystem:<br />
<math>\begin{align}
\vec\omega
=&[\dot\alpha\sin(\beta)\sin(\gamma)+\dot\beta\cos(\gamma)]\hat{g}_1
+[\dot\alpha\sin(\beta)\cos(\gamma)-\dot\beta\sin(\gamma)]\hat{g}_2
+[\dot\alpha\cos(\beta)+\dot\gamma]\hat{g}_3
\\=&[\underbrace{\dot\alpha\sin(\beta)\sin(\gamma)+\dot\beta\cos(\gamma)}_{\omega_3}]\hat{h}_3+[\underbrace{\dot\alpha\sin(\beta)\cos(\gamma)-\dot\beta\sin(\gamma)}_{\omega_1}]\hat{h}_1
+[\underbrace{\dot\alpha\cos(\beta)+\dot\gamma}_{\omega_2}]\hat{h}_2
\,.\end{align}</math><br />
Nun kann die Winkelgeschwindigkeit <math>\dot\alpha</math> mit <math>\dot\gamma=0</math> aus <math>\omega_2
=\dot\alpha\cos(\beta)+\dot\gamma
=\dot\alpha\cos(\beta)</math> bestimmt werden zu<br />
<math>\dot\alpha
=
\frac{\omega_2}{\cos(\beta)}
=\frac{\frac{L}{I_2}\tanh(at)}{\tanh(at)}
=\frac{L}{I_2}
\,.</math><br />
Die Achse um die der Winkel ''β'' dreht ist <math>\hat{u}_\beta=\cos(\gamma)\hat{h}_3-\sin(\gamma)\hat{h}_1</math> und der Meridian hat somit die Richtung<br />
<math>\hat{m}=\hat{h}_2\times\hat{u}_\beta=\cos(\gamma)\hat{h}_1+\sin(\gamma)\hat{h}_3\,.</math><br />
Die Rate der 2-Achse ist<br />
<math>\dot{\hat h}_2=\vec\omega\times\hat{h}_2=\omega_1\hat{h}_3-\omega_3\hat{h}_1\,.</math><br />
Mit den obigen Zwischenergebnissen und den [[Formelsammlung Trigonometrie#Gegenseitige Darstellung|trigonometrischen Formeln]] berechnet sich der Richtungswinkel zwischen Meridian und der Rate des 2-Vektors zu der Konstanten<br />
<math>\begin{align}
\cos\eta
=&\frac{\dot{\hat h}_2\cdot\vec{m}}{|\dot{\hat h}_2||\vec{m}|}
=\frac{\omega_1\sin(\gamma)-\omega_3\cos(\gamma)}{\sqrt{\omega_1^2+\omega_3^2}}
=\frac{\left[\tan(\gamma)-\frac{\omega_3}{\omega_1}\right]\cos(\gamma)}
{\sqrt{1+\frac{\omega_3^2}{\omega_1^2}}}
=\frac{\tan(\gamma)-\frac{I_1}{I_3}\tan(\gamma)}
{\sqrt{1+\frac{I_1^2}{I_3^2}\tan^2(\gamma)}\sqrt{1+\tan^2(\gamma)}}
\\=&
\frac{\frac{I_3-I_1}{I_3}\sqrt{\frac{I_3(I_2-I_1)}{I_1(I_3-I_2)}}}
{\sqrt{1+\frac{I_1^2}{I_3^2}\frac{I_3(I_2-I_1)}{I_1(I_3-I_2)}}\sqrt{1+\frac{I_3(I_2-I_1)}{I_1(I_3-I_2)}}}
=\sqrt{\frac{(I_3-I_2)(I_2-I_1)}{I_2 (I_1+I_3-I_2)}}
\end{align}</math><br />
Der Bruch in der Wurzel ist positiv und kleiner als eins:<br />
<math>\frac{(I_3-I_2)(I_2-I_1)}{I_2 (I_1+I_3-I_2)}=1-\frac{I_1I_3}{I_2 (I_1+I_3-I_2)}<1.</math>
|}
 
== Beispiel rotierendes Pendel ==
[[Datei:rotpendel.png|mini|Abb. 10: Ein um die senkrechte z-Achse rotierendes Pendel]]
Mit einem rotierenden Pendel wird hier ein [[sphärisches Pendel]] gemeint, das um eine Achse, die durch seinen Aufhängepunkt geht, rotiert, siehe Abb. 10. Üblicher Weise werden solche sphärische Pendel mit [[Punktmasse]]n modelliert und mit dem Lagrange-Formalismus behandelt. Hier soll der Pendelkörper eine ausgedehnte und mit Massenträgheit ausgestattete Kugel sein und die Kreiselgleichung angewendet werden.
 
Bei einem rotierenden Pendel muss die Winkelgeschwindigkeit einen kritischen Wert überschreiten, damit eine Gleichgewichtslage ohne Winkelbeschleunigungen möglich ist. Um eine solche Gleichgewichtslage sind kleine harmonische Schwingungen möglich.
 
Das ergibt sich aus den Kreiselgleichungen wie folgt: Das rotierende Pendel bestehe der Einfachheit halber aus einer mit Masse ''m'' und Massenträgheitsmoment ''I'' ausgestatteten Kugel, die in der Entfernung ''r'' vom Drehpunkt fest an einem starren Pendelarm mit vernachlässigbarer Masse befestigt ist und mit der konstanten Winkelgeschwindigkeit ''ω'' um die vertikale z-Achse kreist. Bei einer Kugel sind alle Richtungen Hauptachsen und so werde die Richtung zum Aufhängepunkt als 1-Richtung definiert und die 2-Richtung sei dazu senkrecht, radial nach außen orientiert. Die 3-Richtung ist die zur 1-2-Ebene senkrechte Umfangsrichtung. Wegen der starren Verbindung zum Pendelarm ist <math>\dot\alpha=-\omega_3</math>. Der Ortsvektor des Aufhängepunkts ist von der Kugel aus gesehen <math>\vec{r}=r\hat{g}_1</math>. Die konstante vertikale z-Richtung lautet mit dem [[Sinus und Kosinus]] dann
 
:<math>\hat{e}_z=\cos(\alpha)\hat{g}_1+\sin(\alpha)\hat{g}_2\,.</math>
 
Die Winkelgeschwindigkeit hat eine Komponente in z-Richtung und eine in Umfangsrichtung und mit ihr berechnen sich die Zeitableitungen der Basisvektoren:
 
:<math>\begin{align}
\vec\omega=&\omega\hat{e}_z-\dot\alpha\hat{g}_3
=\omega\cos(\alpha)\hat{g}_1+\omega\sin(\alpha)\hat{g}_2-\dot\alpha\hat{g}_3
\\
\dot{\hat{g}}_1=&\vec\omega\times\hat{g}_1=-\dot\alpha\hat{g}_2-\omega\sin(\alpha)\hat{g}_3
\\
\dot{\hat{g}}_2=&\vec\omega\times\hat{g}_2=\dot\alpha\hat{g}_1+\omega\cos(\alpha)\hat{g}_3
\\
\dot{\hat{g}}_3=&\vec\omega\times\hat{g}_3=\omega\sin(\alpha)\hat{g}_1-\omega\cos(\alpha)\hat{g}_2
\,.\end{align}</math>
 
Weil die Winkelgeschwindigkeit ''ω'' konstant sein soll, <math>\dot\alpha</math> dies jedoch im Allgemeinen nicht ist, ist der Drehimpuls <math>\vec L=I\vec\omega</math> hier im Allgemeinen ''nicht'' konstant.
 
Die [[Gewichtskraft]] der Kugel ist das Produkt aus ihrer Masse und der [[Schwerebeschleunigung]] ''g'' und wird im Aufhängepunkt von einer entgegengesetzt gleichgroßen Aufhängekraft ''mg'' getragen, die ein Moment
 
:<math>\vec{M}_g=\vec{r}\times mg\hat{e}_z=mgr\sin(\alpha)\hat{g}_3</math>
 
im [[Gravizentrum|Schwerpunkt]] der Kugel hervorruft. Ein mit der Kugel bewegter Beobachter befindet sich in einem [[Beschleunigtes Bezugssystem|beschleunigten Bezugssystem]] und muss deshalb auf ein Teilchen mit Masse ''μ'' eine Kraft <math>\mu(-\ddot{\vec r})</math> aufbringen, damit das Teilchen relativ zu ihm ruht. Der Beobachter erklärt sich das mit einer Scheinkraft <math>\mu\ddot{\vec r}</math>, die am Teilchen angreift. Das gilt auch für die Kugel als ganzes. Entsprechend wirkt aus Sicht des Beobachters auf die Kugel eine Scheinkraft
 
:<math>\vec{F}_b
:=m\ddot{\vec r}
=mr\ddot{\hat{g}}_1
=mr\{-[{\dot\alpha}^2+\omega^2\sin^2(\alpha)]\hat{g}_1
+[\omega^2\sin(\alpha)\cos(\alpha)-\ddot\alpha]\hat{g}_2
-2\dot\alpha\omega\cos(\alpha)\hat{g}_3\}
\,.</math>
 
Diese wird nach dem Prinzip [[Actio und Reactio]] mit umgekehrtem Vorzeichen im Lager abgetragen und bringt dort ein entsprechendes scheinbares Moment auf die Kugel auf:
 
:<math>\begin{align}
\vec{M}_b
:=&
\vec{r}\times(-\vec{F}_b)
=
-2mr^2\dot\alpha\omega\cos(\alpha)\hat{g}_2
+mr^2[\ddot\alpha-\omega^2\sin(\alpha)\cos(\alpha)]\hat{g}_3
\,.\end{align}</math>
 
Ein Moment <math>\vec{M}_e</math> mit Komponenten in 1-und 2-Richtung muss eingeleitet werden, damit die Kugel nicht um die Stabachse dreht und eine gleichbleibende Winkelgeschwindigkeit ''ω'' in z-Richtung besitzt. Dieses Drehmoment bedingt eine zeitliche Änderung des Drehimpulses. Die Kreiselgleichungen in 1-und 2-Richtung dienen nur der Bestimmung dieses Moments <math>\vec{M}_e</math>, das hier jedoch nicht interessiert. Die Zwangskraft, die für den gleichbleibenden Abstand der Kugel vom Lager sorgt, verursacht, weil sie in Richtung der Stabachse weist, kein Moment. Um die 3-Richtung kann die Kugel frei drehen und die dritte Komponente der Kreiselgleichung <math>I\dot{\vec\omega}=\vec{M}_g+\vec{M}_b+\vec{M}_e</math> liefert dafür die Bedingung
 
:<math>\begin{align}
I\dot{\omega}_3=-I\ddot\alpha=&mgr\sin(\alpha)+mr^2[\ddot\alpha-\omega^2\sin(\alpha)\cos(\alpha)]
\\\rightarrow
(I+mr^2)\ddot\alpha=&mr\sin(\alpha)[\omega^2r\cos(\alpha)-g]
\,.\end{align}</math>
 
=== Gleichgewichtslagen ===
In Gleichgewichtslagen ohne Winkelbeschleunigungen ergibt sich aus der letzten Gleichung ''mr'' sin(''α'')=0 – dann liegt der Schwerpunkt der Kugel auf der z-Achse – oder:
 
:<math>\cos(\alpha)=\frac{g}{\omega^2r}\,.</math>
 
Die Winkelgeschwindigkeit ''ω'' muss wegen


:<math>
:<math>
\cos(\alpha)\le1
\ddot\delta+\frac{B-A}{C}\mu^2\cos^2(\varphi_0)\delta=0
\quad\rightarrow\quad
</math>&nbsp;&nbsp;&nbsp;&nbsp;mit&nbsp;&nbsp;&nbsp;&nbsp;<math>
\frac{g}{\omega^2r}\le1
\sin(\varphi_0)=\frac{mgs}{(A-B)\mu^2}
\quad\rightarrow\quad
\omega\ge\sqrt{\frac{g}{r}}
</math>
</math>


einen kritischen Wert überschreiten, damit eine Gleichgewichtslage ohne Winkelbeschleunigungen mit positivem Winkel im Bereich 0° < ''α'' < 180° möglich ist. Wegen <math>\tfrac{g}{\omega^2r}>0</math> ist der Winkel bei Gleichgewichtslagen sogar auf den Bereich 0° ≤ ''α'' < 90° eingeschränkt.
Beim gestreckten Kreisel ist ''B&nbsp;>&nbsp;A'' und der "Rückstellkoeffizient" vor δ immer positiv, weswegen der gestreckte Kreisel kleine Schwingungen um Gleichgewichtslagen ausführen kann. Beim abgeplattenten Kreisel ist wegen ''A&nbsp;>&nbsp;B'' der Rückstellkoeffizient negativ. Daher kann der abgeplattete Kreisel keine Schwingungen um Gleichgewichtslagen abseits der Senkrechten ausführen, was im Einklang mit den Ergebnissen aus der [[#Energiebetrachtung|Energiebetrachtung]] ist.


=== Energiebetrachtung ===
== Siehe auch ==
Die dritte Kreiselgleichung kann nach Multiplikation mit <math>\dot\alpha</math> einmal integriert werden:
* [[Poinsotsche Konstruktion]]: grafische Beschreibung der momentenfreien Bewegung.
* [[Physikalisches Pendel]]


:<math>\begin{align}
== Einzelnachweise ==
(I+mr^2)\ddot\alpha\dot\alpha
<references>
&=\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{I+mr^2}{2}{\dot\alpha}^2\right)=\ldots
<ref name="truesdell">
\\\ldots=
{{Literatur
[m\omega^2r^2\sin(\alpha)\cos(\alpha)-mgr\sin(\alpha)]\dot\alpha
| Autor=[[Clifford Truesdell]]
&=
| Hrsg=[[Gesellschaft für Angewandte Mathematik und Mechanik]]
\frac{\mathrm{d}}{\mathrm{d}t}\left[\frac{m}{2}\omega^2r^2\sin^2(\alpha)+mgr\cos(\alpha)\right]
| Titel=Die Entwicklung des Drallsatzes
\\
| Sammelwerk=[[Zeitschrift für Angewandte Mathematik und Mechanik]]
\rightarrow
| Reihe=Heft 4/5
E&=
| Band=44
\frac{I+mr^2}{2}{\dot\alpha}^2
| Datum=1964-04
-\frac{m}{2}\omega^2r^2\sin^2(\alpha)
| Seiten=149 – 158
-mgr\cos(\alpha)
| Online=http://onlinelibrary.wiley.com/doi/10.1002/zamm.19640440402/abstract
=\text{const.}
| DOI=10.1002/zamm.19640440402}}
\end{align}</math>
</ref>
 
</references>
Die [[Integrationskonstante]] ''E'' ist die Energie des Pendels im rotierenden System: Der erste Term auf der rechten Seite ist die [[Rotationsenergie]] der Drehung um die 3-Achse, der zweite Term das [[Zentrifugalkraft#Zentrifugalpotential|Zentrifugalpotential]] der Drehung um die z-Achse und der letzte Term die [[potentielle Energie]] der Kugel.<ref name="Eckelt">{{Internetquelle |autor=P. Eckelt |hrsg=Institut für Theoretische Physik an der Westfälischen Wilhelms-Universität Münster |url=http://pauli.uni-muenster.de/tp/fileadmin/lehre/skripte/eckelt/thmech.pdf |format=PDF |sprache=deutsch |titel=Theoretische Mechanik |seiten=11 bis 13 |datum=2000 |zugriff=2016-07-16 |kommentar=siehe auch die dort angegebenen Quellen}}</ref>
 
=== Schwingungen ===
Die dritte Kreiselgleichung kann um einen Punkt ''α''<sub>0</sub> linearisiert werden. Dazu wird ''α''=''α''<sub>0</sub>+''δ'' mit konstantem ''α''<sub>0</sub> und kleiner Abweichung ''δ'' angenommen. Dann ist sin(''δ'')≈''δ'', cos(''δ'')≈1 und mit den [[Formelsammlung Trigonometrie #Additionstheoreme|Additionstheoremen]] entwickelt sich:
 
:<math>\begin{align}
(I+mr^2)\ddot\alpha=(I+mr^2)\ddot\delta
=&
\frac{m}{2}\omega^2r^2\sin(2\alpha_0+2\delta)-mgr\sin(\alpha_0+\delta)
\\\approx&
\frac{m}{2}\omega^2r^2[\sin(2\alpha_0)+2\cos(2\alpha_0)\delta]
-mgr[\sin(\alpha_0)+\cos(\alpha_0)\delta]
\\\rightarrow
\ddot\delta+\frac{m\omega^2r^2}{I+mr^2}
\underline{\left[\frac{g}{\omega^2r}\cos(\alpha_0)-\cos(2\alpha_0)\right]}\delta
=&
\frac{m\omega^2r^2}{I+mr^2}\left[\cos(\alpha_0)-\frac{g}{\omega^2r}\right]\sin(\alpha_0)
\end{align}</math>
 
Bei ''α''<sub>0</sub>=180°, also am oberen Totpunkt, ist die unterstrichene Differenz negativ und eine Schwingung mithin nicht möglich. Deswegen ist der obere Totpunkt eine instabile Gleichgewichtslage.
 
Am unteren Totpunkt bei ''α''<sub>0</sub>=0° gilt:
* Wenn <math>\omega^2r < g</math>, dann ist der unterstrichene Term positiv und es können kleine Schwingungen stattfinden. Der untere Totpunkt ist in diesem Fall eine stabile Gleichgewichtslage.
* Wenn <math>\omega^2r>g</math>, dann ist der unterstrichene Term negativ und der untere Totpunkt somit eine instabile Gleichgewichtslage. Hier findet eine [[Pitchfork-Bifurkation]] statt.<ref name="Eckelt" />
 
Wenn ''α''<sub>0</sub> eine Gleichgewichtslage ist, dann entfällt die auslenkende Kraft, und es ergibt sich die Schwingungsgleichung
 
:<math>\ddot\delta+\frac{mgr}{I+mr^2}\left(\frac{\omega^2r}{g}-\frac{g}{\omega^2r}\right)\delta=0\,.</math>
 
Um eine Gleichgewichtslage ist eine (kleine) Schwingung immer möglich, weil der Term in den Klammern dann positiv ist.
 
== Siehe auch ==
* [[Poinsotsche Konstruktion]] liefert eine geometrische Beschreibung der Kreiselbewegung
* [[Trägheitsellipsoid]] informiert über den Zusammenhang von Trägheits-, Energie- und Drallellipsoid


== Literatur ==
== Literatur ==
* {{Literatur
* {{Literatur
  |Autor=Herbert Goldstein, Charles P. Poole, Jr, John L. Safko
| Autor=Herbert Goldstein, Charles P. Poole, Jr, John L. Safko
  |Titel=Klassische Mechanik
| Titel=Klassische Mechanik
  |Auflage=3.
| Auflage=3.
  |Verlag=Wiley-VCH
| Verlag=Wiley-VCH
  |Ort=Weinheim
| Ort=Weinheim
  |Datum=2006
| Datum=2006
  |ISBN=3-527-40589-5}}
| ISBN=3-527-40589-5}}
* {{Literatur
| Autor=K. Magnus
| Titel=Kreisel
| TitelErg=Theorie und Anwendungen
| Verlag=Springer
| Ort=Berlin / Heidelberg / New York
| Datum=1971
| Seiten=49
| ISBN=3-540-05198-8}}
* {{Literatur
* {{Literatur
  |Autor=V. I. Arnold
| Autor=[[Richard Grammel| R. Grammel]]
  |Titel=Mathematical Methods of Classical Mechanics
| Titel=Der Kreisel
  |Auflage=2.
| TitelErg=Seine Theorie und seine Anwendungen
  |Verlag=Springer
| Verlag=Vieweg Verlag
  |Ort=New-York / Berlin / Heidelberg / London / Paris / Tokyo
| Ort=Braunschweig
  |Datum=1989
| Datum=1920
  |ISBN=3-540-96890-3}}
| Seiten=45
| Online=https://archive.org/details/derkreiselseine00gramgoog
| Kommentar=„Schwung“ bedeutet Drehimpuls, „[[Drehstoß]]“ etwa Drehmoment und „Drehwucht“ Rotationsenergie
| DNB=451641280}}<br/>oder<br/>{{Literatur
| Autor=R. Grammel
| Titel=Der Kreisel. Seine Theorie und seine Anwendungen
| Band=1: Die Theorie des Kreisels
| Auflage=2. überarb.
| Verlag=Springer
| Ort=Berlin / Göttingen / Heidelberg
| Datum=1950
| Seiten=23
| DNB=451641299}}
* {{Literatur
* {{Literatur
  |Autor=K. Magnus
| Autor=V. I. Arnol’d (В. И. Арнолъд)
  |Titel=Kreisel
| Titel=Mathematische Methoden der klassischen Mechanik
  |TitelErg=Theorie und Anwendungen
| Verlag=Birkhäuser Verlag
  |Verlag=Springer
| Ort=Basel
  |Ort=Berlin / Heidelberg / New York
| Datum=1988
  |Datum=1971
| Seiten=95 f.
  |ISBN=3-540-05198-8}}
| ISBN=978-3-0348-6670-5
| DOI=10.1007/978-3-0348-6669-9
| Online={{Google Buch|BuchID=pkqgBgAAQBAJ|Seite=95}}
| Zugriff=2018-02-14
| Originaltitel=Математическе методы классическоя механики
| Originalsprache=ru
| Originaljahr=1979
| Originalort=Moskau
| Übersetzer=Prof. Dr. Peter Möbius, TU Dresden
}}<br/>oder<br/>{{Literatur
| Autor=V. I. Arnol’d
| Titel=Mathematical Methods of Classical Mechanics
| Auflage=2.
| Verlag=Springer
| Ort=New-York / Berlin / Heidelberg / London / Paris / Tokyo
| Datum=1989
| Seiten=150
| ISBN=3-540-96890-3}}
* {{Literatur
* {{Literatur
  |Autor=R. Grammel
| Autor=Eugene Leimanis
  |Titel=Der Kreisel. Seine Theorie und seine Anwendungen
| Titel=The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point
  |Band=2
| Verlag=Springer Verlag
  |Auflage=2. überarb.
| Ort=Berlin, Heidelberg
  |Verlag=Springer
| Datum=1965
  |Ort=Berlin / Göttingen / Heidelberg
| ISBN=3-642-88414-8
  |Datum=1950
| Seiten=6
  |Kommentar=Schwung=Drehimpuls, Drehstoß=Drehmoment, Drehwucht=Rotationsenergie
| Sprache=en
  |Online={{archive.org|derkreiselseine00gramgoog}}
| Online={{Google Buch|BuchID=s8rsCAAAQBAJ|Seite=6}}
  |DNB=451641280}}
| Abruf=2019-12-27
| DOI=10.1007/978-3-642-88412-2}}


== Weblinks ==
== Weblinks ==
{{Commonscat|Spinning tops|Kreisel}}
* [http://www.ialms.net/sim/ Interaktive Animationen von Kreisel- und Pendelbewegungen] (englisch).
* [http://www.ialms.net/sim/ Interaktive Animationen von Kreisel- und Pendelbewegungen] (englisch).
== Einzelnachweise ==
<references />


{{Normdaten|TYP=s|GND=4347881-5}}
{{Normdaten|TYP=s|GND=4347881-5}}


[[Kategorie:Klassische Mechanik]]
[[Kategorie:Kreiseltheorie]]
[[Kategorie:Wikipedia:Artikel mit Video]]
[[Kategorie:Leonhard Euler als Namensgeber]]
[[Kategorie:Leonhard Euler als Namensgeber]]

Aktuelle Version vom 6. September 2021, 06:56 Uhr

Die Euler’schen Kreiselgleichungen oder uneindeutig Euler’schen Gleichungen sind Bewegungsgleichungen für die Rotation eines starren Körpers. Es sind die Komponenten des für den Starrkörper in seinem Hauptachsensystem aufgeschriebenen Drallsatzes und stellen die wichtigste Grundgleichung der Kreiseltheorie dar.

Wird der Körper einem Drehmoment ausgesetzt, entwickeln sich Kreiselwirkungen, die versuchen, die Eigendrehung mit der erzwungenen Drehung in Deckung zu bringen[1]. Die Kreiselwirkungen sind die summierten Drehmomente der Eulerkräfte und Zentrifugalkräfte an allen Massenpunkten des Körpers. Das Moment und die Kreiselwirkungen befinden sich im dynamischen Gleichgewicht, was die Kreiselgleichungen ausdrücken:

$ {\begin{aligned}M_{1}=&\Theta _{1}{\dot {\omega }}_{1}+(\Theta _{3}-\Theta _{2})\omega _{2}\omega _{3}={\dot {L}}_{1}+\left({\frac {1}{\Theta _{2}}}-{\frac {1}{\Theta _{3}}}\right)L_{2}L_{3}\\M_{2}=&\Theta _{2}{\dot {\omega }}_{2}+(\Theta _{1}-\Theta _{3})\omega _{3}\omega _{1}={\dot {L}}_{2}+\left({\frac {1}{\Theta _{3}}}-{\frac {1}{\Theta _{1}}}\right)L_{3}L_{1}\\M_{3}=&\Theta _{3}{\dot {\omega }}_{3}+(\Theta _{2}-\Theta _{1})\omega _{1}\omega _{2}={\dot {L}}_{3}+\left({\frac {1}{\Theta _{1}}}-{\frac {1}{\Theta _{2}}}\right)L_{1}L_{2}\end{aligned}} $

Darin sind jeweils für $ k=1,2,3 $

$ M_{k} $ die von außen angreifenden Drehmomente,
$ \Theta _{k} $ die Hauptträgheitsmomente,
$ L_{k}=\Theta _{k}\omega _{k} $ die Drehimpulse,
$ \omega _{k} $ die Winkelgeschwindigkeiten und
$ {\dot {\omega }}_{k} $ die Winkelbeschleunigungen

im Hauptachsensystem. Gelegentlich wird auch die dazu gehörige Vektorgleichung[2]

$ {\vec {M}}=\mathbf {\Theta } \cdot {\dot {\vec {\omega }}}+{\vec {\omega }}\times \mathbf {\Theta } \cdot {\vec {\omega }}={\frac {\mathrm {d} _{r}}{\mathrm {d} t}}{\vec {L}}+{\vec {L}}\cdot \mathbf {\Theta } ^{-1}\times {\vec {L}} $

mit dem Trägheitstensor $ \mathbf {\Theta } $ als Euler’sche Kreiselgleichung angegeben. Hier bildet „·“ die Vektortransformation, „ד das Kreuzprodukt und $ {\tfrac {\mathrm {d} _{r}}{\mathrm {d} t}} $ die relative Zeitableitung im Hauptachsensystem.

Die Drehmomente, Hauptträgheitsmomente und Drehimpulse werden mit einem Bezugspunkt berechnet, für den sich der Massenmittelpunkt oder ein unbeschleunigter, in einem Inertialsystem ruhender Stützpunkt eignen, siehe Drallsatz am starren Körper.

Die ersten Summanden auf den rechten Seiten, bestehend aus den Winkelbeschleunigungen und Drehimpulsänderungen, resultieren aus den Kreiselwirkungen der Euler-Kräfte und die anderen, in den Winkelgeschwindigkeiten und Drehimpulsen quadratischen Terme berücksichtigen die Kreiselwirkungen der Zentrifugalkräfte. Wenn die Bewegung bekannt ist, dann können aus diesen Gleichungen die Momente berechnet werden, die im Bezugspunkt eingeleitet werden müssen, damit der Körper die vorgegebene Bewegung ausführt.

Die Kreiselgleichungen wurden von Leonhard Euler 1750 aufgestellt und später zum Drallsatz weiterentwickelt.[3]

Spezialfälle

Euler-Poisson-Gleichungen

Die Euler-Poisson-Gleichungen sind die spezifischen Kreiselgleichungen für den schweren Kreisel, bei dem das äußere Moment von der Schwerkraft herrührt. Die klassische Kreiseltheorie ist fast ausschließlich dem schweren Kreisel mit Stützpunkt gewidmet und es wurde viel Aufwand in das Auffinden exakter Lösungen gesteckt. Eine Auflistung einiger dieser Lösungen[4] findet sich im Hauptartikel.

Kugelkreisel

Ein Kugelkreisel ist ein Kreisel mit drei identischen Hauptträgheitsmomenten Θ, sodass sich die Kreiselgleichungen dann auf

$ {\vec {M}}=\Theta {\dot {\vec {\omega }}} $

reduzieren. Die Winkelbeschleunigung ist beim Kugelkreisel also parallel zum angreifenden Moment. Beim Kugelkreisel sind die Fliehkräfte im Körper immer im mechanischen Gleichgewicht. Ein Vergleich mit den Bewegungsgleichungen bei einer Translationsbewegung zeigt, dass der Kugelkreisel das genaue Analogon des Massenpunkts bei Rotationsbewegungen ist.

Ebene Bewegungen

Bei einer ebenen Bewegung um eine Hauptträgheitsachse, beispielsweise die 3-Achse, entfallen Drehungen und Momente um die 1- und 2-Achsen, und die Gleichungen reduzieren sich auf

$ M_{3}=\Theta _{3}{\ddot {\varphi }}\,, $

wobei φ der Drehwinkel um die 3-Achse ist.

Lösungen der Kreiselgleichungen bei ebenen Bewegungen

Im ebenen Fall sind die Kreiselgleichungen oftmals analytisch lösbar, wofür die beiden folgenden Fälle Beispiele sind.

Anstoß einer Billardkugel

Abb. 1: Anstoß einer Billardkugel parallel zur Tischplatte

Parallel zur Tischplatte soll eine Billardkugel mit Radius r, Masse m und Massenträgheitsmoment Θ so angestoßen werden, dass sie nicht über den Tisch rutscht, siehe Abb. 1. Es stellt sich die Frage, in welcher Höhe h über der Platte die Kraft F eingeleitet werden muss, damit für das schlupflose Rollen keine Reibkraft am Tisch notwendig ist.

Die exzentrisch an der Kugel angreifende horizontale Kraft entwickelt ein Moment M = -(h-r)F um den Massenmittelpunkt, das die Kugel gemäß der Kreiselgleichung

$ M=-(h-r)F=\Theta {\ddot {\varphi }} $

in Drehung versetzt. Das Moment ist negativ, weil es entgegen der Zählrichtung des Drehwinkels φ wirkt. Außerdem beschleunigt die Kraft die Kugel gemäß dem Gesetz „Kraft gleich Masse mal Beschleunigung“:

$ F=m{\ddot {x}}\,. $

Die Beschleunigung $ {\ddot {x}} $ ist parallel zum Tisch in Richtung der Kraft. Die Bedingung für schlupfloses Rollen

$ {\ddot {x}}=-r{\ddot {\varphi }} $

schließt das Gleichungssystem für die drei Unbekannten h, φ und x ab. Damit berechnet sich

$ -(h-r)F=\Theta {\ddot {\varphi }}=-{\frac {\Theta }{r}}{\ddot {x}}=-{\frac {\Theta }{mr}}F\quad \rightarrow \quad h=r+{\frac {\Theta }{mr}}\,. $

Bei einer massiven homogenen Kugel ist das Massenträgheitsmoment Θ = 2⁄5mr² und somit

$ h={\frac {7}{5}}r={\frac {7}{10}}d\,, $

wobei d = 2r der Durchmesser der Kugel ist.

Ein eine schiefe Ebene hinabrollendes Rad

Abb. 2: Ein eine schiefe Ebene hinab rollendes Rad.

In einer ebenen Bewegung rolle ein Rad mit Radius r, Masse m und Massenträgheitsmoment Θ eine mit dem Winkel α geneigte Ebene unter Einfluss einer Schwerebeschleunigung g hinab, siehe Abb. 2. Weil sich das Rad dabei auch translatorisch bewegt, geht auch seine Masse in die Beschleunigung ein. Die Beschleunigung wächst jedoch, wenn das Massenträgheitsmoment abnimmt.

Aufgrund des schlupflosen Abrollens entsteht am Aufstandspunkt des Rades eine Reibkraft R, die das Rad in Drehung versetzt, denn es entspricht einem Moment M=-r R um den Massenmittelpunkt. Das Moment ist negativ, weil es entgegen der Zählrichtung des Drehwinkels φ arbeitet. Damit lautet die Kreiselgleichung im ebenen Fall:

$ -rR=\Theta {\ddot {\varphi }}\,. $

Die auf das Rad hangabwärts wirkende Komponente F der Gewichtskraft mg hat die Größe F=mgsin(α). Ihr entgegen steht die Reibkraft, sodass nach dem zweiten newtonschen Gesetz gilt:

$ F-R=m{\ddot {x}}\quad \rightarrow \quad R=mg\sin(\alpha )-m{\ddot {x}}\,, $

worin $ {\ddot {x}} $ die hangabwärts zählende Beschleunigung des Rades und sin die Sinusfunktion ist. Die Bedingung für schlupfloses Rollen $ {\ddot {x}}=-r{\ddot {\varphi }} $ schließt das Gleichungssystem für die drei Unbekannten R, φ und x ab und es ergibt sich

$ {\ddot {x}}={\frac {mr^{2}}{\Theta +mr^{2}}}g\sin(\alpha ) $

Ein hangabwärts, reibungsfrei rutschender Klotz erfährt die Beschleunigung $ {\ddot {x}}=g\sin(\alpha ) $, die größer ist als die des Rades, denn beim Rad wird ein Teil der potentiellen Energie in Rotationsenergie umgesetzt, die dann für die Translation fehlt.

Beispiel: Fliehkraftpendel

Ein bemerkenswerter Anwendungsfall der Euler’schen Kreiselgleichungen ist die "Perle auf rotierendem Kreisring im Schwerefeld"[5][6], das konische oder Fliehkraftpendel, denn es hat überraschende Eigenschaften. In Worten der Kreiseltheorie handelt es sich um einen schweren Kreisel, der in einem Punkt festgehalten wird und bei dem die Eigendrehung um die Pendelachse durch äußere Momente verhindert und die Präzessionsgeschwindigkeit konstant gehalten wird. Komplexere Eigenschaften treten bei beliebiger Lage des Massenmittelpunkts und anfänglicher Ausrichtung der Hauptachsen auf. Vereinfachungen ergeben sich mit Massenmittelpunkt auf der 1-Achse und permanent horizontaler 3-Achse des Hauptachsen­systems.

Kinematik

Die in der Kreiseltheorie üblichen Definitionen der Winkel und Winkelgeschwindigkeiten werden übernommen. Insbesondere wird die z-Komponente der 2-Achse

$ n_{2}=\sin(\vartheta )\cos(\varphi )=\cos(\varphi ) $

bei horizontaler 3-Achse (ϑ ≡ 90°) benötigt, die identisch mit der 2-Komponente des Einheitsvektors ist, der vertikal nach oben weist. Die Funktionen sin und cos bilden den Sinus und Kosinus.

Die Winkelgeschwindigkeiten lauten unter den hiesigen Bedingungen:

$ {\begin{aligned}\mu :=&{\dot {\psi }}=\omega _{1}\sin(\varphi )+\omega _{2}\cos(\varphi )={\text{const.}}\\{\dot {\vartheta }}=&\omega _{1}\cos(\varphi )-\omega _{2}\sin(\varphi )\equiv 0\\\omega _{1}=&\mu \sin(\varphi ),\;\omega _{2}=\mu \cos(\varphi ),\;\omega _{3}={\dot {\varphi }}\end{aligned}} $

Der Winkel ϑ ist unveränderlich, wenn er anfangs keine Zeitableitung hat und dauerhaft keine Beschleunigung erfährt.

Kinetik

Die 1- oder Pendelachse trägt im Abstand s > 0 vom Fixpunkt den Massenmittelpunkt, dessen Gewichtskraft mg somit ein Schweremoment auf das Pendel ausübt. Zusätzlich zu diesem Schweremoment wirken äußere Momente M1,2 in 1- bzw. 2-Richtung des Hauptachsensystems, um Winkelbeschleunigungen von ϑ und μ zu unterdrücken. Die Kreiselgleichungen in 1- und 2-Richtung dienen nur der Bestimmung dieser Momente, die hier nicht interessieren. Bemerkenswert ist jedoch, dass diese Drehmomente eine zeitliche Änderung des vertikalen Drehimpulses verursachen[5], der bei schweren Kreiseln immer konstant ist.

Um die horizontale 3-Richtung kann das Pendel frei drehen und das Schweremoment in dieser Richtung ist -mgsn2 = -mgs cos(φ), siehe Kinematik oben und Euler-Poisson-Gleichungen. Damit liefert die dritte der Kreiselgleichungen

$ M_{3}=-mgs\cos(\varphi )=C{\dot {\omega }}_{3}+(B-A)\omega _{1}\omega _{2} $

die Bewegungsgleichung

$ {\ddot {\varphi }}={\frac {1}{C}}[(A-B)\mu ^{2}\sin(\varphi )-mgs]\cos(\varphi ) $ 
 
 (*)
 

Darin sind A, B und C die Hauptträgheitsmomente um die 1-, 2- bzw. 3-Achse.

Gleichgewichtslagen

Im Gleichgewicht verschwindet in (*) die Winkelbeschleunigung:

$ C{\ddot {\varphi }}=[(A-B)\mu ^{2}\sin(\varphi )-mgs]\cos(\varphi )=0 $.

Anders als beim sich selbst überlassenen Lagrange-Kreisel ist eine Präzession mit waagerechter Achse (φ = 0) nicht möglich. Mangels Eigendrehung gibt es hier keine Kreiselwirkung, die das Schweremoment ausgleichen könnte. Das Gleichgewicht mit lotrechter 1-Achse (φ = ±90°) ist allen Kreiseln zugänglich – auch dem Kugelkreisel, der nur dort Gleichgewicht findet. Bei A ≠ B ergeben sich die Gleichgewichtslagen aus

$ \left[\sin(\varphi )-{\frac {mgs}{(A-B)\mu ^{2}}}\right]\cos(\varphi )=0 $

Wenn A - B dasselbe Vorzeichen wie sin(φ) hat, kann der Term in der eckigen Klammer null werden. Dazu muss

$ |\sin(\varphi )|\leq 1\quad \Rightarrow \quad |\mu |\geq {\sqrt {\frac {mgs}{|A-B|}}}=:\mu _{c} $

erfüllt sein. Das Pendel muss eine kritische Drehgeschwindigkeit μc überschreiten, damit diese Gleichgewichtslage abseits der Senkrechten existiert. Beim abgeplatteten Kreisel weist die 1-Achse im Gleichgewicht nach oben (ist A > B und sin(φ) > 0) und beim gestreckten nach unten (A < B und sin(φ) < 0).

Analog zum symmetrischen Kreisel wird das Pendel hier und im folgenden abgeplattet genannt, wenn A > B, und gestreckt, wenn B > A.

Energiebetrachtung

Multiplikation der Bewegungsgleichung (*) mit $ {\dot {\varphi }} $ ermöglicht eine Zeitintegration:

$ E={\frac {C}{2}}{\dot {\varphi }}^{2}+{\frac {B-A}{2}}\mu ^{2}\sin ^{2}(\varphi )+mgs\sin(\varphi ) $

Die Integrationskonstante E ist die Energie des Pendels im rotierenden System:[5]

  • der erste Summand trägt die Rotationsenergie um die 3-Achse bei,
  • der zweite Summand ist das Zentrifugalpotential der Präzession und
  • der dritte Summand steht für die Lageenergie im Schwerefeld der Erde.

Die Energie und ihre Ableitungen (·)' nach φ ergeben sich mit der Abkürzung $ z:={\tfrac {mgs}{(A-B)\mu ^{2}}} $ zu

$ {\begin{aligned}E=&{\frac {C}{2}}{\dot {\varphi }}^{2}+(B-A)\mu ^{2}{\bigg (}{\frac {\sin ^{2}(\varphi )}{2}}-z\sin(\varphi ){\bigg )}\\E'=&(B-A)\mu ^{2}[\sin(\varphi )-z]\cos(\varphi )\\E''=&(B-A)\mu ^{2}[1+z\sin(\varphi )-2\sin ^{2}(\varphi )]\end{aligned}} $

Beim gestreckten Kreisel ist B > A und z < 0 und beim abgeplattenten Kreisel ist B < A sowie z > 0. Stabilität liegt in einem Energieminimum vor, wo E' = 0 und E" > 0 ist. Die Energie ist in Gleichgewichtslagen stationär: bei sin(φ) = z oder cos(φ) = 0, wo sin(φ) = -1 oder sin(φ) = +1 ist:

Gleichgewichtslage mit sin(φ) = z
Hier ist E" = (A-B)μ²(z²-1). Diese Bewegung ist beim gestreckten Kreisel stabil, wenn z 2 < 1, also immer, und beim abgeplatteten, wenn z 2 > 1, also nie.
Hängendes Pendel sin(φ) = -1
Hier ist E" = (A-B)μ²(1+z). Der untere Totpunkt ist beim abgeplatteten Kreisel stabil, wenn z > -1, also immer, und beim gestreckten, wenn z < -1, also |μ| < μc. Bei zunehmendem μ durchläuft das gestreckte Pendel bei μ = μc eine subkritische Pitchfork-Bifurkation[5], wo die stabile Lage am unteren Totpunkt instabil wird und zwei stabile Gleichgewichtslagen mit sin(φ) = z entstehen. Im Gegensatz dazu ist der lotrecht hängende Lagrange-Kreisel immer stabil[7], siehe dort.
Aufrechtes Pendel sin(φ) = +1
Hier ist E" = (A-B)μ²(1-z). Der obere Totpunkt ist beim gestreckten Kreisel stabil, wenn z > 1, also nie, und beim abgeplatteten, wenn z < 1 oder |μ| > μc. Bei zunehmendem μ durchläuft das abgeplattete Pendel bei μ = μc eine superkritische Pitchfork-Bifurkation, wo die instabile Lage am oberen Totpunkt stabil wird und zwei neue instabile Gleichgewichtslagen mit sin(φ) = z entstehen.

Schwingungen

Die Gleichung (*) kann um Gleichgewichtslagenφ0, wo z = sin(φ0) ist, linearisiert werden. Dazu wird φ = φ0+δ mit konstantem φ0 und kleiner Abweichung δ angenommen. Die Drehbeschleunigung

$ C{\ddot {\varphi }}=C{\ddot {\delta }}=(A-B)\mu ^{2}\sin(\varphi _{0}+\delta )\cos(\varphi _{0}+\delta )-mgs\cos(\varphi _{0}+\delta ) $

entwickelt sich mit den Additionstheoremen und sin(δ) ≈ δ, cos(δ) ≈ 1 zur Schwingungsgleichung

$ {\ddot {\delta }}+{\frac {B-A}{C}}\mu ^{2}\cos ^{2}(\varphi _{0})\delta =0 $    mit    $ \sin(\varphi _{0})={\frac {mgs}{(A-B)\mu ^{2}}} $

Beim gestreckten Kreisel ist B > A und der "Rückstellkoeffizient" vor δ immer positiv, weswegen der gestreckte Kreisel kleine Schwingungen um Gleichgewichtslagen ausführen kann. Beim abgeplattenten Kreisel ist wegen A > B der Rückstellkoeffizient negativ. Daher kann der abgeplattete Kreisel keine Schwingungen um Gleichgewichtslagen abseits der Senkrechten ausführen, was im Einklang mit den Ergebnissen aus der Energiebetrachtung ist.

Siehe auch

  • Poinsotsche Konstruktion: grafische Beschreibung der momentenfreien Bewegung.
  • Physikalisches Pendel

Einzelnachweise

  1. ↑ Grammel (1920), S. 70.
  2. ↑ In der Tensoralgebra kann auf Klammerungen verzichtet werden:
    $ ({\vec {L}}\cdot \mathbf {\Theta } ^{-1})\times {\vec {L}}={\vec {L}}\cdot (\mathbf {\Theta } ^{-1}\times {\vec {L}})={\vec {L}}\cdot \mathbf {\Theta } ^{-1}\times {\vec {L}} $
  3. ↑ Clifford Truesdell: Die Entwicklung des Drallsatzes. In: Gesellschaft für Angewandte Mathematik und Mechanik (Hrsg.): Zeitschrift für Angewandte Mathematik und Mechanik (= Heft 4/5). Band 44, April 1964, S. 149 – 158, doi:10.1002/zamm.19640440402 (wiley.com).
  4. ↑ Magnus (1971), S. 109.
  5. ↑ 5,0 5,1 5,2 5,3 P. Eckelt: Theoretische Mechanik. (PDF) Institut für Theoretische Physik an der Westfälischen Wilhelms-Universität Münster, 2000, S. 11 bis 13, abgerufen am 16. Juli 2016 (siehe auch die dort angegebenen Quellen).
  6. ↑ Arnold (1988), S. 95 f.
  7. ↑ Grammel (1920), S. 111.

Literatur

  • Herbert Goldstein, Charles P. Poole, Jr, John L. Safko: Klassische Mechanik. 3. Auflage. Wiley-VCH, Weinheim 2006, ISBN 3-527-40589-5.
  • K. Magnus: Kreisel. Theorie und Anwendungen. Springer, Berlin / Heidelberg / New York 1971, ISBN 3-540-05198-8, S. 49.
  • R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. Vieweg Verlag, Braunschweig 1920, DNB 451641280, S. 45 (archive.org – „Schwung“ bedeutet Drehimpuls, „Drehstoß“ etwa Drehmoment und „Drehwucht“ Rotationsenergie).
    oder
    R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. 2. überarb. Auflage. 1: Die Theorie des Kreisels. Springer, Berlin / Göttingen / Heidelberg 1950, DNB 451641299, S. 23.

  • oder
    V. I. Arnol’d: Mathematical Methods of Classical Mechanics. 2. Auflage. Springer, New-York / Berlin / Heidelberg / London / Paris / Tokyo 1989, ISBN 3-540-96890-3, S. 150.

Weblinks

Commons: Kreisel – Sammlung von Bildern, Videos und Audiodateien
Abgerufen von „https://www.cosmos-indirekt.de/physik_137/index.php?title=Eulersche_Gleichungen_(Kreiseltheorie)&oldid=17308“

Die News der letzten Tage

02.05.2024
Exoplaneten | Thermodynamik | Astrophysik
Wolken auf der Nachtseite: Neues vom Exoplaneten WASP-43b
Ein Forschungsteam hat mit Hilfe des Weltraumteleskops James Webb eine Temperaturkarte des heißen Gasriesen-Exoplaneten WASP-43b erstellt. Der nahe gelegene Mutterstern beleuchtet ständig eine Hälfte des Planeten und lässt die Temperaturen auf glühende 1250 Grad Celsius ansteigen.
30.04.2024
Kernphysik | Quantenoptik
Erstmals Atomkern mit Laser angeregt
Der seit Jahrzehnten gesuchte „Thorium-Übergang“ wurde nun von TU Wien und der PTB Braunschweig erstmals mit Lasern gezielt angeregt. Damit ist der Weg frei für völlig neue Präzisions-Technologien, bis hin zur Atomkern-Uhr.
25.04.2024
Quantenoptik
Molekulare Fingerabdrücke jenseits der Nyquist-Frequenz
Die ultraschnelle Laserspektroskopie ermöglicht die Erfassung dynamischer Vorgänge auf extrem kurzen Zeitskalen, und macht sie damit zu einem sehr nützlichen Instrument für viele wissenschaftliche und industrielle Anwendungen.
25.04.2024
Teilchenphysik | Quantencomputer
Ressourcenschonendes Quantencomputing
Eine internationale Kollaboration hat einen bedeutenden Durchbruch in der Quantentechnologie erzielt: Die Forscher*innen demonstrierten mit einer neuartigen ressourceneffizienten Plattform erfolgreich die Quanteninterferenz zwischen mehreren einzelnen Photonen.
24.04.2024
Atomphysik | Festkörperphysik | Quantenphysik
Überraschende Umkehr in Quantensystemen
Forschende haben topologisches Pumpen in einem künstlichen Festkörper aus kalten Atomen untersucht. Die Atome wurden mit Laserstrahlen gefangen.