Pirouetteneffekt
Der Pirouetteneffekt ist die Steigerung oder Verlangsamung der Rotationsgeschwindigkeit, die sich ergibt, wenn bei einem sich drehenden Objekt die Masse näher zur Rotationsachse gezogen oder von dieser weiter entfernt wird. Im Alltag erfahrbar ist der Effekt bei der namensgebenden Pirouette im Eiskunstlauf. Dabei versetzen sich Eiskunstläufer zunächst bei zur Seite ausgestreckten Armen in Rotation. Wenn die Arme eng an den Körper angelegt werden, verringert sich dadurch das Trägheitsmoment $ \Theta $ der Läufer. Da dabei der Drehimpuls $ L=\Theta \cdot \omega $ erhalten bleibt, nimmt die Winkelgeschwindigkeit $ \omega $ der Rotation zu. Umgekehrt verringert sich die Rotationsgeschwindigkeit, wenn die Arme ausgestreckt werden.
Das gleiche Prinzip nutzen Turner und Turmspringer beim Salto[1] oder bei Schrauben. In der Luft werden Arme und Beine angezogen, um so aus dem beim Absprung erhaltenen Drehimpuls eine möglichst schnelle Drehung zu gewinnen. Eine Öffnung der Haltung vor dem Auftreffen auf den Boden verringert die Drehgeschwindigkeit und erlaubt eine stehende Landung.
Der Pirouetteneffekt tritt auch bei anderen Drehbewegungen auf, beispielsweise bei einem Tornado in der Entstehungsphase. Bei einer Supernova bricht der Innenbereich des Sterns zusammen, der entstehende Neutronenstern hat dann Umdrehungszeiten im Millisekundenbereich.
Physikalische Grundlagen des Pirouetteneffekts
| Physikalische Größe | Formelzeichen | SI-Einheiten |
|---|---|---|
| Drehimpuls | $ L $ | N·m·s, kg·m2/s |
| Geschwindigkeit | $ v $ | m/s |
| Masse | $ m $ | kg |
| Winkelgeschwindigkeit | $ {\omega } $ | rad/s |
| Trägheitsradius | $ i $ | m |
| Rotationsenergie | $ W $ | N·m, kg·m2/s2 |
| Hubarbeit | $ W_{\mathrm {Diff} } $ | N·m, kg·m2/s2 |
Der Drehimpuls $ {\vec {L}} $ lässt sich ausdrücken als Produkt von Trägheitsradius $ i $, Masse $ m $ und Winkelgeschwindigkeit $ {\vec {\omega }} $:
- $ {\vec {L}}=i^{2}\,m\,{\vec {\omega }} $
Aufgrund der Drehimpulserhaltung gilt für ein System ohne äußere Einflüsse und unveränderter Masse, wobei die Indizes $ 1 $ und $ 2 $ zwei Zustände des Systems bezeichnen:
- $ L_{1}=m\cdot i_{1}^{2}\cdot \omega _{1}=m\cdot i_{2}^{2}\cdot \omega _{2}=L_{2} $
Daraus ergibt sich, dass die Winkelgeschwindigkeiten sich antiproportional zu den Quadraten der Trägheitsradien verhalten:
- $ {\frac {i_{1}^{2}}{i_{2}^{2}}}={\frac {\omega _{2}}{\omega _{1}}} $
Für Punktmassen im Abstand $ i $ kann die Umfangsgeschwindigkeit $ v_{1,2}=i_{1,2}\cdot \omega _{1,2} $ an Stelle der Winkelgeschwindigkeit genutzt werden, sodass gilt:
- $ {\frac {i_{1}}{i_{2}}}={\frac {v_{2}}{v_{1}}}. $
Da die Rotationsenergien $ \textstyle W={\frac {m}{2}}\cdot v^{2} $ ist, gilt
- $ {\frac {W_{1}}{W_{2}}}={\frac {\omega _{1}}{\omega _{2}}}={\frac {i_{2}^{2}}{i_{1}^{2}}}. $
Bei konstanter Masse $ m_{1}=m_{2} $ können, wenn beispielsweise Trägheitsradien und eine der Winkelgeschwindigkeiten bekannt sind, mit obiger Formel die andere Winkelgeschwindigkeit, die Rotationsenergien sowie die Hubarbeit $ W_{\mathrm {Diff} }=W_{1}-W_{2} $ berechnet werden.

Die Hubarbeit kann auch direkt ermittelt werden:
- $ {\begin{aligned}W_{\mathrm {Diff} }&={\frac {m}{2}}\cdot \left(\omega _{1}^{2}\cdot i_{1}^{2}-\omega _{2}^{2}\cdot i_{2}^{2}\right)\\&={\frac {m}{2}}\cdot \omega _{1}^{2}\cdot i_{1}^{2}\left(1-{\frac {i_{1}^{2}}{i_{2}^{2}}}\right)\end{aligned}} $
Der Pirouetteneffekt ist ein Wechselspiel zwischen Hubenergie und Rotationsenergie. Die Differenz der Rotationsenergien ist die Hubarbeit, die beim Wechsel auf einen kleineren Radius wieder in Rotationsenergie zurückverwandelt werden kann; d. h., die Verringerung des Radius erfordert einen wachsenden Kraftaufwand über die Distanz $ i_{2}-i_{1} $. Bei der Vergrößerung des Radius wird die in der Rotation gebundene Energie frei.
Der Trägheitsradius eines Massenpunkt ist sein Abstand von der Rotationsachse. Bei mehreren Massepunkten wird dieser effektive Abstand bestimmt, indem die Beiträge alle Massen $ m_{l} $ mit ihren jeweiligen Radien $ r_{l} $ aufsummiert werden:
- $ i^{2}\sum _{l}m_{l}=\sum _{l}r_{l}^{2}\cdot m_{l} $
Für starre Körper, die nicht um eine Hauptträgheitsachse rotieren, was bei Massenpunkten, die untereinander wechselwirken und sich nicht in einer Ebene senkrecht zur Drehachse befinden, im Allgemeinen der Fall ist, muss die Drehimpulserhaltung
- $ {\begin{aligned}{\vec {L}}_{1}&={\vec {L}}_{2}\\\mathbf {\Theta } _{1}{\vec {\omega }}_{1}&=\mathbf {\Theta } _{2}{\vec {\omega }}_{2}\end{aligned}} $
mit den Trägheitstensoren $ \mathbf {\Theta } _{1} $ und $ \mathbf {\Theta } _{2} $ angenommen werden.
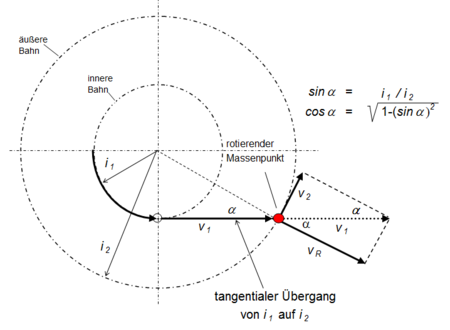
Trigonometrische Erklärung
Der rotierende Massenpunkt wird vom Radius $ i_{1} $ zum Radius $ i_{2} $ versetzt, etwa durch Verlängern der Verbindung mit dem Drehpunkt. Die Masse bewegt sich tangential geradlinig weiter bis zur äußeren Bahn. Dabei nimmt sie die Geschwindigkeit $ v_{1} $ und die Rotationsenergie aus dem inneren Radius als kinetische Energie bis zum Radius $ i_{2} $ mit:
- $ W_{1}={\frac {1}{2}}m\,v_{1}^{2} $
Auf dem äußeren Radius kann die Geschwindigkeit $ v_{1} $ in die Komponenten $ v_{2} $ und $ v_{\mathrm {R} } $ zerlegt werden. $ v_{2} $ ist die neue Umfangsgeschwindigkeit, und $ v_{\mathrm {R} } $ ist die gedachte Radialgeschwindigkeit, die jedoch, weil sie auf dem neuen Radius = Null ist, in Hubarbeit umgerechnet werden kann.
Vorlage:Tabellenstile
| Physikalische Größe | Formel |
|---|---|
| $ \cos(\alpha )={\sqrt {1-(i_{1}/i_{2})^{2}}} $ | |
| Umfangsgeschwindigkeit2 | $ v_{2}=\sin(\alpha )\,v_{1} $ |
| Radialvektor | $ v_{\mathrm {R} }=\cos(\alpha )\,v_{1} $ |
| Rotationsenergiedifferenz | $ W_{\mathrm {Diff} }={\frac {1}{2}}m\,v_{\mathrm {R} }^{2} $ |
Die Art des Übergangs auf einen anderen Radius spielt für den Endzustand keine Rolle. In der Praxis wird die Bewegung spiralförmig verlaufen, im Ergebnis entsprechen aber die Werte für Energie und Geschwindigkeit dem vereinfachten Beispiel.
Einzelnachweise
- ↑ Sportmechanik, Abschnitt „Drehimpuls und Drehimpulserhaltung“, Abb. 70 auf S. 78.
Literatur
- Günther Bäumler: Sportmechanik: Grundlagen für Studium und Praxis. BLV Verlagsgesellschaft, München Wien Zürich 1981, ISBN 3-405-12435-2.
- David Halliday, Robert Resnick, Jearl Walker: Physik. 2. Auflage. WILEY-VCH Verlag GmbH & co. KGaA, Berlin 2009, ISBN 978-3-527-40645-6.