Methode der harmonischen Balance
- Stabilitätstheorie
- Systemdarstellung
- Schwingungsdynamik
- Nichtlineare Dynamik
Die Methode der harmonischen Balance – angewandt in der Regelungstechnik – besteht darin, die Dauerschwingungen eines nichtlinearen zurückgekoppelten dynamischen Systems durch eine harmonische Schwingung anzunähern. Dabei wird das nichtlineare Teilsystem durch eine Beschreibungsfunktion dargestellt. Mit der Methode werden die Parameter des Schwingungszustandes und die Stabilitätsgrenze berechenbar. N.M. Krylow und N.N. Bogoljubow verwendeten bereits 1937 den Begriff Harmonische Balance für dieses von ihnen entwickelte Verfahren.
Ein nichtlineares dynamisches System kann nach dem Hammerstein-Modell in ein statisches nichtlineares System und ein dynamisches lineares System zerlegt werden. Wird der Ausgang des linearen Systems negativ auf den Systemeingang des nichtlinearen Systems zurückgeführt und damit zu einem Regelkreis geschaltet, kann das Gesamtsystem schwingen.
Mit dem Verfahren der Harmonischen Linearisierung wird von einem schwingenden nichtlinearen Regelkreis ausgegangen, dessen Ausgangssignal durch das Tiefpass-Verhalten der Regelstrecke eine angenäherte harmonische Schwingung ausführt, die in den Systemeingang negativ zurückgeführt wird. Nur unter diesen Bedingungen darf das nichtlineare statische System als lineares Übertragungsglied mit der Beschreibungsfunktion $ N(A) $ definiert werden, welche nur von der sinusförmigen harmonischen Eingangsschwingung mit der Amplitude $ A $ und nicht von der komplexen Frequenz $ \mathrm {j} \omega $ abhängt.
Mit der Gleichung der Harmonischen Balance werden die Beziehungen der Beschreibungsfunktion $ N(A) $ des statischen nichtlinearen Systems und des dynamischen linearen Systems $ G_{0}(\mathrm {j} \omega ) $ in ein Verhältnis gesetzt. Daraus lassen sich die zwei kritischen Systemgrößen des harmonisch schwingenden Regelkreises – die Eingangsamplitude $ A $ und die kritische Frequenz $ \omega _{\mathrm {krit} } $ an der Stabilitätsgrenze – errechnen oder grafisch nach dem Zwei-Ortskurven-Verfahren bestimmen.
Die Anwendung der Harmonischen Balance zur Prüfung von nichtlinearen Regelkreisen mit dem anschaulichen Zwei-Ortskurven-Verfahren darauf, wann Dauerschwingungen auftreten und wie diese sich vermeiden lassen, erfordert keine besonderen mathematischen Kenntnisse. Die benötigte Beschreibungsfunktion des nichtlinearen statischen Systems zur Konstruktion der Ortskurve ist in vielen Varianten in der Fachliteratur der Regelungstechnik dargestellt. Dies gilt insbesondere für die verschiedenen Formen der Kennlinienregler.
Grundlagen des linearen und nichtlinearen schwingenden Systems
Streng genommen sind fast alle Regelkreise nichtlineare Systeme. Die häufigste statische Nichtlinearität ist die Sättigungseigenschaft der Stellgröße des Reglers. So ist bei einem P-Regler trotz erhöhter Regelabweichung keine Signalerhöhung der Stellgröße möglich, weil eine Signalbegrenzung vorliegt. Für diesen einfachen Fall der Signalbegrenzung wird die Regelgröße bei einem Führungsgrößensprung oder einer plötzlich auftretenden Störgröße der Sollwert der Regelgröße nicht so schnell erreicht wie ohne Stellgrößen-Begrenzung.
Wird die P-Verstärkung eines stabilen Regelkreises weiter erhöht, dann wird – vorausgesetzt, die Regelstrecke ist ein lineares System höherer als 2. Ordnung – der Regelkreis an der Stabilitätsgrenze f (P-Verstärkung) instabil. Die Regelgröße wird dann mit konstanter oder zunehmender Amplitude schwingen. Dabei ist es nicht gleichgültig, ob eine Stellgrößen-Begrenzung vorliegt oder nicht.
„Dauerschwingungen“ (auch Grenzschwingungen und Grenzzyklen) sind periodische, sinusförmige Zeitvorgänge im eingeschwungenen Zustand mit konstanter Amplitude. Sie unterscheiden sich von auf- und abklingenden Schwingungen.
Ruhelagen und Stabilität
Eine Ruhelage eines dynamischen Systems im schwingungsfreien Zustand ist asymptotisch stabil, wenn nach einer Signalstörung die Ausgangsgröße $ y(t) $ wieder in die Ruhelage zurückkehrt. Ein stabiles System neigt dazu, seinen momentanen Zustand beizubehalten, auch wenn Störungen von außen einwirken. Zu jedem Stabilitätsbereich gehört eine Ruhelage und ein Einzugsbereich der Ruhelage. Hat ein nichtlinearer Regelkreis nur eine Ruhelage, so kann man annehmen, dass seine Ausgangsgröße $ y(t) $ global asymptotisch stabil ist, sofern keine Dauerschwingungen auftreten.
Nichtlineare dynamische Systeme sind im Gegensatz zu linearen Systemen von Anfangsbedingungen und des Eingangssignals der statischen Nichtlinearität abhängig. Je nach Funktion der statischen Nichtlinearität kann stabiles und instabiles Verhalten auftreten. Nichtlineare Systeme können bei Einsatz von sogenannten Kennlinien-Reglern im Regelkreis gewollte Schwingungen hervorrufen. Solche stationären Dauerschwingungen werden auch als Grenzschwingungen bezeichnet. Grenzschwingungen können stabil, instabil und semistabil sein.
Nichtlineare Regelsysteme können im Gegensatz zu linearen Systemen mehrere Ruhelagen haben. Ein Pendel wird mit seinen Massen der potentiellen und kinetischen Energien durch eine Differenzialgleichung 2. Ordnung beschrieben, in der der Winkel $ \varphi $ als 2. Ableitung und nichtlinear auftritt. Bewertet man den Winkel des Befestigungspunktes mit 90°, dann hat das Pendel eine Ruhelage bei 270° und einen Einzugsbereich der Ruhelage > 90° und < 90° und eine instabile Ruhelage von 90° im Koordinatensystem.
Ein nichtlineares dynamisches System mit der Ausgangsgröße $ y(t) $ hat folgendes Verhalten bei Auslenkung aus einer instabilen Ruhelage:
- $ y(t) $ geht in eine andere Ruhelage über,
- $ y(t) $ strebt in Richtung $ \infty $,
- $ y(t) $ macht eine Dauerschwingung.
Mit der Harmonischen Balance lässt sich klären, ob Grenzschwingungen auftreten können und ob sie stabil oder instabil sind und welche Frequenz und (Eingangs-)Amplitude sie haben.
Stabilitätsgrenze des linearen dynamischen Systems
Ein dynamisches System verhält sich linear, wenn die Wirkungen zweier linear überlagerter Eingangssignale sich am Ausgang des Systems in gleicher Weise linear überlagern. Das System verhält sich linear, wenn es das Superpositionsprinzip (Siehe auch: Superpositionsprinzip der Physik) und das Verstärkungsprinzip erfüllt.
Ein Übertragungssystem ist intern stabil, wenn alle (Teil-)Übertragungsfunktionen nur Pole in der linken s-Halbebene haben. Ein Übertragungssystem gilt als extern stabil, wenn jedes beliebige beschränkte Eingangssignal an dem System auch ein beschränktes Ausgangssignal hervorruft. (Siehe BIBO-Stabilität)
Die Stabilitätsgrenze eines linearen Regelkreises ist nach dem vereinfachten Stabilitätskriterium von Nyquist erreicht, wenn die Ortskurve des Frequenzgangs (Siehe auch PT2-Glied) des offenen Regelkreises genau den kritischen Punkt −1 der Abszisse des Realteils schneidet. Für Werte des Schnittpunktes $ \operatorname {Re} <-1 $ entstehen aufklingende Schwingungen des geschlossenen Regelkreises.
Damit gilt für die Stabilität der Grenzschwingung der kritischen Frequenz $ \omega _{\mathrm {krit} } $ des offenen Regelkreises:
- $ F_{0}(\mathrm {j} \omega _{\mathrm {krit} })=-1 $.
Zur Ermittlung der Ortskurve wird der komplexe Frequenzgang in Real- und Imaginärteil zerlegt und für verschiedene Werte der Frequenz $ \omega $ in der Gaußschen Zahlenebene eingetragen.
- Aus einer gegebenen Übertragungsfunktion $ G(s) $ oder einem Frequenzgang $ G(\mathrm {j} \omega ) $ in Produktdarstellung wird der Nenner des Frequenzgangs als Polynom ausmultipliziert und in Realteil und Imaginärteil geordnet.
- Damit der imaginäre Anteil im Nenner des Frequenzgangs verschwindet, muss der Real- und Imaginärteil des Nenners mit sich selbst aber mit umgekehrten Vorzeichen mit der Frequenzganggleichung multipliziert werden.
- Beispiel: $ (x+\mathrm {j} \omega )\cdot (x-\mathrm {j} \omega )=x^{2}-\mathrm {j} ^{2}\omega ^{2}=x^{2}+\omega ^{2} $
- [ Anmerkung: $ (\mathrm {j} \omega )^{2}=-\omega ^{2};(\mathrm {j} \omega )^{3}=-\mathrm {j} \omega ^{3} $ ]
- Der Zähler wird mit dem Real- und Imaginärteil des Nenners multipliziert, damit die Gleichung mit der ursprünglichen Aussage unverändert ist.
- Der Zähler wird nach Realteil und Imaginärteil geordnet.
Konstruktion einer Ortskurve des Frequenzgangs
Gegeben: Übertragungsfunktion 3. Ordnung mit globalem I-Verhalten und der Verstärkung K.
- $ G(s)={\frac {K}{s\cdot (T_{1}\cdot s+1)(T_{2}\cdot s+1)}} $
- $ G(\mathrm {j} \omega )={\frac {K}{\mathrm {j} \omega \cdot (T_{1}\cdot \mathrm {j} \omega +1)(T_{2}\cdot \mathrm {j} \omega +1)}}={\frac {K}{-(T_{1}+T_{2})\cdot \omega ^{2}+\mathrm {j} \cdot \left(\omega -T_{1}\cdot T_{2}\cdot \omega ^{3}\right)}} $
Wird der Realteil des Nenners mit der Hilfsgröße $ a=-(T_{1}+T_{2})\omega ^{2} $ und der Imaginärteil des Nenners mit der Hilfsgröße $ b=\omega -T_{1}T_{2}\omega ^{3} $ bezeichnet, kann der Frequenzgang $ G(\mathrm {j} \omega ) $ für den Realteil und den Imaginärteil wie folgt berechnet werden:
Zunächst werden die Zahlenwerte der Hilfsgrößen $ a $ und $ b $ als Funktion von $ \omega =0 $ bis $ \omega =\infty $ in Stufen von $ \omega $-Werten errechnet und in die unten stehende Gleichung des Frequenzgangs $ G(\mathrm {j} \omega ) $ eingesetzt. Die so errechneten realen und imaginären Anteile des Frequenzgangs werden in das Diagramm der Gaußschen Zahlenebene als Ortskurve des Frequenzgangs eingetragen.
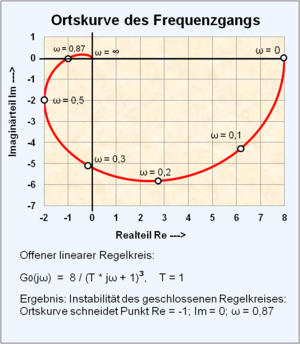
Ortskurve des Frequenzgangs $ G(j\omega ) $
| $ G(\mathrm {j} \omega )={\frac {K\cdot a}{a^{2}+b^{2}}}-\mathrm {j} {\frac {K\cdot b}{a^{2}+b^{2}}} $ |
Zahlenbeispiel der Stabilitätsgrenze eines linearen Regelkreises:
Gegeben: Offener Regelkreis mit einem P-Regler: $ K=8 $ und einer Regelstrecke 3. Ordnung, $ T=1 $:
- $ \ G_{0}(s)={\frac {8}{(T\cdot s+1)^{3}}} $
Gesucht: Verhalten der Sprungantwort für die Führungsgröße $ w(t)=1 $ des geschlossenen Regelkreises.
Nach dem Schließen des Regelkreises mit dieser ungünstigen Regelstrecke mit drei gleichen Zeitkonstanten wird bereits bei der Verstärkung $ K=8 $ die Stabilitätsgrenze für eine konstante Amplitude der Regelgröße erreicht. Die Ortskurve durchläuft als $ f(\omega =2\pi f) $ beginnend bei $ f(\omega =0) $ mit dem Wert $ \operatorname {Re} =8,\omega =0;\operatorname {Im} =0 $ den 4., 3. und 2. Quadranten und schneidet die Abszisse des Realteils bei genau $ \operatorname {Re} =-1,\operatorname {Im} =0 $.
Die Form der Ortskurve ändert sich nicht, solange die drei Zeitkonstanten einen beliebigen aber untereinander den gleichen Wert $ (T_{1}=T_{2}=T_{3}=T) $ haben. Die Größe der Zeitkonstante $ T $ hat dann eine Bedeutung, wenn das Zeitverhalten des Regelkreises z. B. als Sprungantwort der Führungsgröße dargestellt werden soll. Drei gleiche Zeitkonstanten in einer Regelstrecke mit drei Verzögerungsgliedern stellen regelungstechnisch das ungünstigste Zeitverhalten bezüglich der Stabilität des Regelkreises dar.
Wird die Verstärkung $ K>8 $ erhöht, dann treten progressiv zunehmend größere Amplituden mit steigender Zeit auf. Die Ortskurve des Frequenzgangs schneidet die Abszisse bei Werten < −1. Wird die Verstärkung $ K<8 $ reduziert, dann nehmen die Amplituden der Regelgröße einen aperiodischen gedämpften Verlauf und die Regelgröße nimmt nach der Einschwingzeit einen konstanten Wert an. Die Ortskurve schneidet die Abszisse bei Werten > −1.
Besteht die Regelstrecke nur aus einem Verzögerungssystem 2. Ordnung mit einem P-Regler beliebig hoher Verstärkung, kann es theoretisch nicht zu Dauerschwingungen kommen, weil die Ortskurve des Frequenzgangs nur den 4. und 3. Quadranten der gaußschen Zahlenebene durchläuft und den kritischen Punkt $ \operatorname {Re} =-1 $ nicht treffen kann.
Anmerkung: Für die Berechnung des Schwingungszustandes eines nichtlinearen dynamischen Systems nach dem Zwei-Ortskurven-Verfahren ist die Kenntnis der Konstruktion der Ortskurve des Frequenzgangs des linearen Systems erforderlich!
Verhalten des nichtlinearen dynamischen Systems
Dynamische Systeme werden durch Differenzialgleichungen (DGL) beschrieben. Enthält die DGL oder die gesuchte Funktion oder deren Ableitungen eine Potenz $ n>1 $ oder Produkte der gesuchten Funktion oder Winkelfunktionen, Logarithmen usw. in den Argumenten, handelt es sich um eine nichtlineare DGL und das System verhält sich nichtlinear. Nichtlineare Differenzialgleichungen sind nur in sehr seltenen Ausnahmefällen analytisch lösbar. Sie können aber mittels der numerischen zeitdiskreten Methoden oder mit kommerziellen Rechenprogrammen (Simulink) relativ einfach berechnet werden.
Bei einem nichtlinearen statischen System kann die Übertragungskennlinie als eine in weiten Grenzen sich ändernde Verstärkung angesehen werden. Das System antwortet auf ein sinusförmiges Eingangssignal meist mit einer Verzerrung der Schwingung des Eingangssignals gleicher Frequenz und einer Phasenverschiebung. Lediglich ein symmetrisches Zweipunkt-Element (Zweipunktregler) ohne Hysterese, ohne Totzone und Signalbegrenzung antwortet auf eine sinusförmige Eingangsschwingung mit einer Rechteckschwingung der gewählten Rechteck-Amplitude $ u(t)=\pm U_{\mathrm {max} }=\pm d $ der gleichen Frequenz ohne eine Phasenverschiebung.
($ d $ ist der Kennlinien-Hilfspunkt der nichtlinearen Kennlinie zu einer sinusförmigen Eingangs-Schwingung $ e(t) $)
Das einfache symmetrische Zweipunkt-Element mit der Rechteck-Amplitudenhöhe $ \pm d $ definiert sich als Signumfunktion mit $ u(t) $ als Ausgangsgröße:
- $ u(t)=f[e(t)]=d\cdot \operatorname {sign} [e(t)]{\begin{cases}d&{\text{für}}\;e(t)>0,\ {\text{stabil}}\\0&{\text{für}}\;e(t)=0,\ {\text{instabil}}\\-d&{\text{für}}\;e(t)<0,\ {\text{stabil.}}\end{cases}} $
Das Zweipunkt-Element hat zwei Ruhelagen. Es erzeugt in Abhängigkeit von dem Eingangssignals $ e(t) $ zwei Stellgrößen. Der Zustand $ u(t)=0 $, für $ e(t)=0 $ ist nur dann ein stationärer Wert, wenn dem Zweipunkt-Element eine Totzone $ {\mathit {TZ}}=c $ ($ c $ ist Kennlinien-Hilfspunkt) eingerichtet wird. Damit würde aus dem Zweipunkt-Element ein Dreipunkt-Element entstehen.
Sonderfälle sind statische nichtlineare Systeme mit quadratischer oder exponentieller Kennlinie. Ein sinusförmig erregtes System mit quadratischer Kennlinie antwortet mit einer Sinusschwingung der doppelten Frequenz und Gleichanteil (verschobener Arbeitspunkt); ein System mit exponentieller Kennlinie antwortet mit einem sinusähnlichen Impuls mit großem Oberwellenanteil.
Wird ein nichtlineares dynamisches System 2. und höherer Ordnung durch ein sinusförmiges Eingangssignal $ e(t) $ angeregt, antwortet es meistens mit einer angenähert sinusförmigen Schwingung gleicher Frequenz, aber anderer Amplitude und einer Phasenverschiebung. Ist das statische nichtlineare System ein schaltender Regler, so wird in einem Regelkreis trotz steiler Impulsflanken des rechteckförmigen Regler-Ausgangssignals $ \pm U_{\mathrm {max} } $ bei genügend großer Frequenz von $ e(t) $ und $ u(t) $ durch das Tiefpassverhalten des linearen dynamischen Systems ein angenähert sinusförmiges Ausgangssignal $ y(t) $ erreicht.
Durch dieses Verhalten ist die „Harmonische Linearisierung“ begründet: die Rechteckschwingung mit ihrem großen Oberwellen-Anteil als Eingangsgröße $ u(t) $ wird nur in ihrer Grundschwingung entsprechender Amplitude berücksichtigt. Damit kann das nichtlineare statische System $ N $ in Abhängigkeit von der Amplitude $ e_{\mathrm {max} }=A $ der Sinusschwingung des Eingangssignals $ e(t) $ beschrieben werden.
Nichtlineare Systeme sind häufig einzigartig, jedoch können aus dem nichtlinearen statischen System Verhaltensweisen definiert werden, die bei gegebenen Parametern eine System-Beschreibungsfunktion erlauben. Darunter fallen Elemente mit Begrenzung, Totzone, Hysterese, progressiver Kennlinie und die sogenannten Kennlinienregler wie Zweipunkt- und Mehrpunktregler, die sich in zahlreichen Varianten wie folgt darstellen:
- Zweipunkt-Element (Zweipunktregler) symmetrisch und unsymmetrisch mit und ohne Hysterese
- Dreipunkt-Element (Dreipunktregler) symmetrisch und unsymmetrisch mit und ohne Hysterese
- Mehrpunkt-Element
- Element mit progressiver Kennlinie symmetrisch und unsymmetrisch
- Element mit degressiver Kennlinie, symmetrisch und unsymmetrisch
- Elemente mit Begrenzung symmetrisch und unsymmetrisch
- Elemente mit Totzone symmetrisch und unsymmetrisch
- Elemente mit Totzone und Begrenzung
- Elemente mit Vorspannung
- Gleichrichter-Element
- Betragselement
Laut der Fachliteratur können bis zu 40 unterschiedliche Beschreibungsfunktionen nichtlinearer statischer Systeme entnommen werden, die das nichtlineare Systemverhalten $ N(A) $ nur für ein periodisches sinusförmiges Eingangssignal $ e(t)=e_{\mathrm {max} }\sin(\omega t) $ mit der Amplitude $ A=e_{\mathrm {max} } $ und das Ausgangssignal $ u(t) $ nur mit der Grundwelle beschreiben.
Harmonische Linearisierung
Festlegung der Signalgrößen, Parameter und Eckwerte der Kennlinien-Strukturen
In der bekannten Fachliteratur der Regelungstechnik sowie in den aktuellen Vorlesungsmanuskripten deutscher Hochschulen findet man für die Harmonische Linearisierung kaum eine identische mathematische Ableitung aus der Fourieranalyse, noch identische System- und Signalbezeichnungen. Ursache sind die verschiedenen Signalbezeichnungen z. B. mit Xe, Xa, E, U, X, Y, der Gleichungsaufbau der Fourieranalyse und die Bezeichnungen der geometrischen Eckpunkte der nichtlinearen Kennlinien.
Die Gleichung der Fourieranalyse und deren Vereinfachung unterscheiden sich durch die unterschiedliche Verwendung der harmonischen Sinus- oder Kosinusschwingung mit und ohne Gleichanteile, unterschiedliche Integrationsgrenzen und unterschiedliche Berechnung der Koeffizienten. Auch sind die Ergebnisse der Beschreibungsfunktionen unter verschiedenen Namen (öfter $ N(A) $, $ N(U_{0}) $, $ B({\hat {X}}e)\, $, $ N({\hat {X}}e)\, $) als Funktion der Amplitude der Eingangsgröße des nichtlinearen Systems mit zahlreichen Kennlinien-Regler-Funktionen nicht übereinstimmend, weil die geometrischen Eckwerte der Kennlinien-Beschreibung mit den Hilfsgrößen (meist $ a,b,c,d $) in unterschiedlicher Weise benutzt werden.
Trotz der unterschiedlichen mathematischen Wege, die zu der Gleichung der Harmonischen Balance führen, ist das Ergebnis überall identisch. Das Verständnis der Ortskurve des Frequenzgangs des linearen Systems ist erforderlich und ebenso das Verständnis der Ortskurve der Beschreibungsfunktion des nichtlinearen statischen Systems. Aus der Fachliteratur können die zahlreichen Beschreibungsfunktionen der nichtlinearen statischen Systeme mit den zugehörigen Skizzen der Kennlinien und der Ortskurven entnommen werden. Die unterschiedlichen geometrischen Eckwerte mit der Kennlinienskizze ($ a,b,c,d $) der Beschreibungsfunktion können leicht den verschiedenen Quellen der Fachliteratur zugeordnet werden.
Nachfolgend wird von den international verwendeten Systemgrößen des Regelkreises ausgegangen: Führungsgröße $ w(t)=0 $, Reglereingangsgröße $ e(t) $, Reglerausgangsgröße (Nichtlinearität) $ u(t) $ und linearer Regelstrecken-Ausgang $ y(t) $. Die folgenden dargestellten mathematischen Ableitungen sind der Fachliteratur[1] nachempfunden.
Methode der harmonischen Linearisierung
Die Methode der Harmonischen Linearisierung geht gemäß dem Hammerstein-Modell von der Annahme aus, dass die von dem nichtlinearen System erzeugten Oberwellen durch das nachfolgende lineare System mit Tiefpassverhalten als unwirksam (gefiltert) werden.
Aus der Sicht der Regelungstechnik wird für ein nichtlineares dynamisches System häufig das Hammerstein-Modell – im Gegensatz zum Wiener-Modell – eingesetzt, weil in vielen Fällen die zum Regler gehörende Stellgröße nichtlinear ist.
Das Verhalten des Reglers als nichtlineares statisches System $ N $ kann durch eine in weiten Grenzen sich ändernde Verstärkung angesehen werden, wodurch bei einem sinusförmigen Eingangssignal $ e(t)=e_{\mathrm {max} }\sin(\omega t) $ eine Signalverzerrung und Phasenverschiebung $ \varphi $ des Ausgangssignals $ u(t)=f[e(t),N(e_{\mathrm {max} })] $ hervorgerufen wird. Häufig ist die Abhängigkeit von $ N(e_{\mathrm {max} }) $ durch bekannte Parameter oder durch die Größe der Amplitude $ e_{\mathrm {max} } $ des sinusförmigen Eingangssignals $ e(t) $ bestimmt, deshalb ist das Großsignal-Verhalten des Systems zu untersuchen, „Stabilität im Großen“. Manche Kennlinienregler sprechen erst an, wenn das Eingangssignal eine Mindestgröße erreicht.
Für eindeutige nichtlineare Kennlinien wie das Zweipunkt-Element, d. h. für jedes statische Eingangssignal $ e(t) $ gibt es nur ein statisches Ausgangssignal $ u(t) $, ist die Beschreibungsfunktion reell, d. h. die Phasenverschiebung $ \varphi =0 $.
Vereinfachung der nichtlinearen Beschreibungsfunktion im Zustand der Dauerschwingung
Die Eingangsgröße $ e(t) $ des statischen nichtlinearen Systems soll eine Sinusschwingung ohne Gleichanteil sein:
- $ e(t)=e_{\mathrm {max} }\cdot \sin(\omega \cdot t) $.
Die Amplitude $ e_{\mathrm {max} } $ der Eingangs-Sinusschwingung wird häufig in der Fachliteratur mit $ e_{\mathrm {max} }=A $ bezeichnet.
Die verzerrte Ausgangsschwingung $ u(t) $ lässt sich als Fourier-Reihe schreiben, als eine Summe aus einem Gleichwert $ a_{0} $ und aus den Sinussignalen der Grundfrequenz $ a_{1}\sin(\omega _{0}t+\phi _{1}) $ und den harmonischen Oberschwingungen als Vielfache der Grundfrequenz:
- $ u(t)=a_{0}+\sum _{n=1}^{\infty }\left[a_{n}\cdot \cos \left({\frac {n2\pi t}{T}}\right)+b_{n}\cdot \sin \left({\frac {n2\pi t}{T}}\right)\right]\quad {\text{mit}}\quad \omega ={\frac {2\pi }{T}}=2\pi f $.
Die Ausgangsgröße $ u(t) $ kann je nach Verhalten des nichtlinearen Systems einen Gleichanteil $ a_{0} $ enthalten. Es interessiert aber nur das Schwingverhalten.
Wenn das nachgeschaltete lineare System $ G(\mathrm {j} \omega ) $ die verzerrte sinusähnliche Eingangsschwingung $ u(t) $ als Tiefpassfilter stark genug dämpft, werden die hohen Frequenzen im Vergleich zu den niedrigeren sehr stark unterdrückt. Für diese Betrachtung werden die Anteile der Oberschwingungen als vernachlässigbar angenommen.
- $ u(t)\approx a_{0}+a_{1}\cos(\omega \cdot t)+b_{1}\sin(\omega \cdot t) $
Die Beschreibungsfunktion des statischen nichtlinearen Systems ergibt sich durch das Verhältnis der Grundwellen des Ausgangssignals $ u_{1}(t) $ zum Eingangssignal $ e_{1}(t) $. Sie berücksichtigt nur die Grundschwingung des Ausgangssignals ohne den Gleichanteil $ a_{0} $.
Eingangssignal:
- $ e_{1}(t)=e_{\mathrm {max} }\cdot \sin(\omega \cdot t) $
Ausgangssignal:
- $ u_{1}(t)=a_{1}\cos(\omega \cdot t)+b_{1}\sin(\omega \cdot t) $
Mit der komplexen Darstellung der beiden Signale ergibt sich die Beschreibungsfunktion nach der Euler-Formel:
- $ \cos(\omega \cdot t)+\mathrm {j} \cdot \sin(\omega \cdot t)=\mathrm {e} ^{\mathrm {j} \omega t} $
- $ (\cos(\omega \cdot t)+\mathrm {j} \cdot \sin(\omega \cdot t))\cdot \mathrm {e} ^{-\mathrm {j} \pi /2}=-\mathrm {j} \cdot \mathrm {e} ^{\mathrm {j} \omega t} $
- $ e_{1}(t)=\operatorname {Re} {(-\mathrm {j} \cdot e_{\mathrm {max} }\cdot \mathrm {e} ^{\mathrm {j} \omega t})}\Rightarrow {\tilde {e}}_{1}(t)=-\mathrm {j} \cdot e_{\mathrm {max} }\cdot \mathrm {e} ^{\mathrm {j} \omega t} $
- $ u_{1}(t)=\operatorname {Re} {((a_{1}-\mathrm {j} \cdot b_{1})\cdot \mathrm {e} ^{\mathrm {j} \omega t})}\Rightarrow {\tilde {u}}_{1}(t)=(a_{1}-\mathrm {j} \cdot b_{1})\cdot \mathrm {e} ^{\mathrm {j} \omega t} $.
Beschreibungsfunktion des nichtlinearen Systems
- $ N(e_{\mathrm {max} })={\frac {{\tilde {u}}_{1}(\mathrm {j} \omega t)}{{\tilde {e}}_{1}(\mathrm {j} \omega t)}}={\frac {(a_{1}-\mathrm {j} \cdot b_{1})\cdot \mathrm {e} ^{\mathrm {j} \omega t}}{-\mathrm {j} \cdot e_{\mathrm {max} }\cdot \mathrm {e} ^{\mathrm {j} \omega t}}} $
Die Eingangsamplitude $ e_{\mathrm {max} } $ der Sinusschwingung des nichtlinearen Systems wird häufig auch mit $ A $ bezeichnet.
| $ N(A)={\frac {b_{1}+\mathrm {j} a_{1}}{A}}={\frac {b_{1}}{A}}+\mathrm {j} {\frac {a_{1}}{A}} $ |
$ a_{1} $ und $ b_{1} $ sind die Koeffizienten der ersten Grundschwingungen des nichtlinearen Systems.
Für die zahlreichen Formen der sogenannten Kennlinienregler lassen sich anhand der Geometrie der Kennlinien mit diesen Koeffizienten (häufig mit $ a,b,c,d $ bezeichnet) die Fourier-Koeffizienten $ a_{1} $ und $ b_{1} $ der nichtlinearen Beschreibungsfunktionen $ N(A) $ errechnen.
- $ a_{1}={\frac {2}{T}}\cdot \int _{-T/2}^{T/2}u(t)\cdot \cos(\omega t)\,\mathrm {d} t\qquad {\text{mit}}\quad \omega ={\frac {2\pi }{T}} $
- $ b_{1}={\frac {2}{T}}\cdot \int _{-T/2}^{T/2}u(t)\cdot \sin(\omega t)\,\mathrm {d} t\qquad {\text{mit}}\quad \omega ={\frac {2\pi }{T}} $
Die Beschreibungsfunktionen sind abhängig von der Funktion des nichtlinearen Kennlinien-Elements.
- Der Ausgang eines symmetrischen Zweipunkt-Elements schwingt als Funktion der Eingangsschwingung synchron mit den Nulldurchgängen ohne Phasenverschiebung.
- Unsymmetrische Mehrpunkt-Elemente (Amplitude $ d\neq \left|-d\right| $) erzeugen einen Gleichanteil.
- Bei Kennlinien-Elementen mit Hysteresefunktionen sind die Beschreibungsfunktionen komplex.
Die Beschreibungsfunktionen kann man als einen „Ersatzfrequenzgang“ eines nichtlinearen Systems bezeichnen. Sie hängt von der Amplitude $ A $ der Eingangsschwingung $ e(t) $ und der Frequenz der Dauerschwingung $ \omega =2\pi f $ ab und wird mit $ N(A,\omega ) $ definiert. Zum Unterschied des linearen Frequenzgangs mit der Abhängigkeit von $ \omega $, ist die Beschreibungsfunktion im Wesentlichen von der Amplitude $ A $ als unabhängige Variable abhängig. Bei rein statischer Nichtlinearität entfällt die Abhängigkeit von der Frequenz. Nachfolgend werden die Beschreibungsfunktionen als frequenzunabhängig für statische Nichtlinearitäten betrachtet als $ N(A) $.
Die Aufstellung und umfangreichen Ableitungen der Beschreibungsfunktionen $ N(A) $ der zahlreichen Kennlinien-Elemente sind der Fachliteratur der Regelungstechnik zu entnehmen. Die jeweiligen Beschreibungsfunktionen $ N(A) $ der nichtlinearen statischen Systeme sind alle als algebraische Funktionen abgeleitet, lediglich die relevanten geometrischen Eckpunkte mit den Buchstaben $ a,b,c,d $ unterscheiden sich, können aber leicht anhand der beigefügten Kennlinien-Skizzen zugeordnet werden.
Aufstellung bekannter Beschreibungsfunktionen von Kennlinien-Elementen
Die nachfolgenden Beschreibungsfunktionen $ N(A) $ gelten nur für Anwendungen im Zustand der Harmonischen Balance.[2]
| Benennung Nichtlineares System |
Beschreibungsfunktion $ N(A)=\operatorname {Re} \left(N(A)\right)+\mathrm {j} \operatorname {Im} \left(N(A)\right) $ |
Nichtlineare Kennlinie und invertierte Ortskurve $ -{\frac {1}{N(A)}} $ |
|---|---|---|
| Zweipunkt-Regler $ u={\begin{cases}-d&{\text{für}}\;e<0\\0&{\text{für}}\;e=0\\d&{\text{für}}\;e>0\end{cases}} $ |
$ {\begin{aligned}\operatorname {Re} \left(N(A)\right)&={\frac {4\cdot d}{\pi \cdot A}}\\\operatorname {Im} \left(N(A)\right)&=0\end{aligned}} $ | 
|
| Zweipunkt-Regler mit Hysterese $ u={\begin{cases}-d&{\text{für}}\;e\leq -c\\-d,d&{\text{für}}\;-c<e<c\\d&{\text{für}}\;c\leq e\end{cases}} $ |
$ {\begin{aligned}\operatorname {Re} \left(N(A)\right)&={\frac {4\cdot d}{\pi \cdot A}}\cdot {\sqrt {1-\left({\frac {c}{A}}\right)^{2}}}\\\operatorname {Im} \left(N(A)\right)&=-{\frac {4\cdot c\cdot d}{\pi \cdot A^{2}}}\\{\text{mit}}\;A\geq c\end{aligned}} $[3] | 
|
| Element mit Begrenzung (Sättigung) $ k=\tan \alpha =d/c $ |
$ {\begin{aligned}\operatorname {Re} \left(N(A)\right)&={\frac {2\cdot d}{\pi \cdot c}}\cdot \arcsin \left({\frac {c}{A}}\right)+{\frac {2\cdot d}{\pi \cdot A}}\cdot {\sqrt {1-\left({\frac {c}{A}}\right)^{2}}}\\\operatorname {Im} \left(N(A)\right)&=0\\{\text{mit}}\;A\geq c\end{aligned}} $ | 
|
| Element mit Totzone $ k=\tan \alpha =d/(c_{0}-c) $ |
$ {\begin{aligned}\operatorname {Re} \left(N(A)\right)&=k-{\frac {2\cdot k}{\pi }}\cdot \arcsin \left({\frac {c}{e}}\right)-{\frac {2\cdot k\cdot c}{\pi \cdot e}}\cdot {\sqrt {1-\left({\frac {c}{A}}\right)^{2}}}\\\operatorname {Im} \left(N(A)\right)&=0\\{\text{mit}}\;A\geq c\end{aligned}} $ | 
|
| Dreipunkt-Regler (= Zweipunkt-Regler mit Totzone) $ u={\begin{cases}-d&{\text{für}}\;e\leq -c\\0&{\text{für}}\;-c<e<c\\d&{\text{für}}\;c\leq e\end{cases}} $ |
$ {\begin{aligned}\operatorname {Re} \left(N(A)\right)&={\frac {4\cdot d}{\pi \cdot A}}\cdot {\sqrt {1-\left({\frac {c}{A}}\right)^{2}}}\\\operatorname {Im} \left(N(A)\right)&=0\\{\text{mit}}\;A\geq c\end{aligned}} $ | 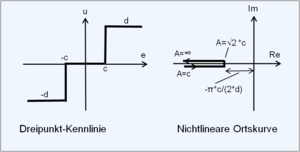
|
Gleichung der Harmonischen Balance
Für das Verfahren der Harmonischen Balance wird der geschlossene Regelkreis an der Stabilitätsgrenze für die Führungsgröße $ w(t)=0 $ betrachtet.
Die Ausgangsgröße des linearen Systems gilt:
- $ \ Y(\mathrm {j} \omega )=G(\mathrm {j} \omega )\cdot U(\mathrm {j} \omega ) $.
Die Nichtlinearität verhält sich im Schwingungsgleichgewicht wie ein lineares Übertragungsglied:
- $ \ U(\mathrm {j} \omega )=N(A)\cdot E(\mathrm {j} \omega )=N(A)\cdot (-Y(\mathrm {j} \omega )) $.
Mit $ E(\mathrm {j} \omega )=-Y(\mathrm {j} \omega ) $ ergibt sich aus den 3 Gleichungen die charakteristische Gleichung des nichtlinearen Regelkreises, die mit Gleichung der Harmonischen Balance bezeichnet wird:
- $ \ G(\mathrm {j} \omega )\cdot N(A)=-1 $.
Die häufigste Schreibweise der Gleichung der Harmonischen Balance lautet:
$ \ G(\mathrm {j} \omega )=-{\frac {1}{N(A)}} $
Wenn eine Dauerschwingung des nichtlinearen Regelkreises existiert, dann stellt sich die Gleichung der Harmonischen Balance als die charakteristische Gleichung der nichtlinearen Regelung dar. Die Lösung der Gleichung der Harmonischen Balance kann formelmäßig-numerisch oder grafisch nach dem Zwei-Ortskurven-Verfahren erfolgen.
Formelmäßige Lösung der Gleichung der Harmonischen Balance
Bei komplizierten nichtlinearen Beschreibungsfunktionen oder linearen Systemen höherer Ordnung kann die formelmäßige Lösung sehr schwierig werden. In diesem Fall wählt man die anschauliche grafische Lösung des Zwei-Ortskurven-Verfahrens.
Die gesuchten unbekannten Größen sind die Amplitude $ A $ der Nichtlinearität und die Frequenz $ \omega $, mit der das nichtlineare dynamische System schwingt.[4]
Die Gleichung der Harmonischen Balance wird umgeformt, um zunächst $ A $ berechnen zu können:
- $ N(A)=-{\frac {1}{G(\mathrm {j} \omega )}} $.
Schreibt man die Gleichung in Realteil und Imaginärteil:
- $ \operatorname {Re} N(A)=-\operatorname {Re} {\frac {1}{G(\mathrm {j} \omega )}} $
- $ \operatorname {Im} N(A)=-\operatorname {Im} {\frac {1}{G(\mathrm {j} \omega )}} $.
Damit ergeben sich zwei reelle Gleichungen. Handelt es sich um eindeutige nichtlineare Kennlinien, d. h. für jede Eingangsgröße existiert eine eindeutige Ausgangsgröße wie bei den Zweipunkt- und Dreipunkt-Elementen, so wird die Beschreibungsfunktion mit dem Imaginärteil zu Null:
- $ \operatorname {Im} {\frac {1}{G(\mathrm {j} \omega )}}=0 $.
Die Lösung des Gleichungssystems vereinfacht sich auf die Lösung zweier getrennter Gleichungen. Zuerst werden die Pole von $ \omega $ des linearen Systems aus $ \operatorname {Im} 1/G(j\omega )=0 $ bestimmt und in die rechte Seite der nachfolgenden Gleichung eingesetzt. So kann $ A $ berechnet werden mit:
- $ \operatorname {Re} N(A)=-\operatorname {Re} {\frac {1}{G(\mathrm {j} \omega )}} $.
Zwei-Ortskurven-Verfahren der Harmonischen Balance
Die grafische Methode ist sehr anschaulich. Man erhält die Amplitude $ A $ und die Frequenz der Dauerschwingung $ \omega $ des nichtlinearen Regelkreises, wenn sich ein Schnittpunkt der beiden Ortskurven des Frequenzgangs $ G(\mathrm {j} \omega ) $ und der negativen invertierten Beschreibungsfunktion $ -1/N(A) $ ergibt. Es lässt sich feststellen, ob es in einem Regelkreis zu Dauerschwingungen kommt und ob mehrere Dauerschwingungen möglich sind.
Die in der Gleichung der Harmonischen Balance dargestellte negative, invertierte Ortskurve der Beschreibungsfunktion $ N(A) $ kann in das gleiche Diagramm der Ortskurve des Frequenzgangs $ G(\mathrm {j} \omega ) $ als $ {\frac {-1}{N(A)}} $ eingetragen werden, mit den Ortskurven-Parametern von $ A $. Schwingt das System, ergibt sich ein Schnittpunkt der beiden Ortskurven. Daraus kann die Amplitude $ A $ und die Frequenz $ \omega =2\pi f $ abgelesen werden.
Je nach Art des nichtlinearen Systems ist die Lage der negativen inversen Ortskurve auf der realen Achse des Koordinatensystems eine Gerade und hat keine imaginären Anteile. Bei nichtlinearen Systemen mit einer Hysterese handelt es sich um eine im negativen imaginären Bereich versetzte Gerade. Bei nichtlinearen Systemen mit Dreipunktregler und Hysterese handelt es sich um ein Kennlinienfeld.
Je nach Art der Ortskurve des Frequenzgangs und der Ortskurve der Beschreibungsfunktion kann es zu mehreren Dauerschwingungen kommen, weil es zu mehreren Schnittpunkten kommen kann. Bei dem Dreipunktregler ist die Ortskurve der Beschreibungsfunktion auf der realen Achse gefaltet (die beiden Äste der Ortskurve überdecken sich), d. h. für eine gegebene Frequenz $ \omega $ können im Schnittpunkt Schwingungen für zwei verschieden große Amplituden $ A $ möglich sein.
Andererseits kann die Ortskurve des Frequenzgangs für lineare Systeme größerer Ordnung den Punkt Re = 0 und Im = 0 umschlingen. Enthält das lineare System eine Totzeit, dann verläuft die Ortskurve des Frequenzgangs spiralförmig um den Punkt Re = 0 und Im = 0, so dass es zu vielen Schnittpunkten und damit zu mehreren Dauerschwingungen unterschiedlicher Amplituden $ A $ und unterschiedlichen Frequenzen $ \omega $ kommen kann.
Handelt es sich bei einem Regelkreis um beispielsweise einem Zweipunktregler und einem linearen System $ G_{0}(s) $ erster oder zweiter Ordnung, kann es laut dem Zwei-Ortskurven-Verfahren nicht zu Dauerschwingungen kommen, weil die Ortskurve des Frequenzgangs nicht in den zweiten Quadranten kommen kann. Leider weiß man durch numerische Berechnung oder aus Erfahrung mit Zweipunktreglern, dass der Regelkreis mit einer Dauerschwingung antwortet. Die Begründung dieses Verhaltens wird damit erklärt, dass die Bedingung der harmonischen Schwingung der Ausgangsgröße $ y(t) $ des Regelkreises mit Tiefpassverhalten nicht erfüllt wird. Die Ausgangsgröße $ y(t) $ ist in diesem Fall keine harmonische Schwingung.
Dagegen können sich die Ortskurven eines Zweipunktreglers mit Hysterese durch die Lage der [-1 / N(A)]-Ortskurve im negativen imaginären Bereich des 3. Quadranten sehr wohl mit der Ortskurve des linearen Systems $ G(\mathrm {j} \omega ) $ 2. Ordnung treffen.
Praxisbeispiel der Harmonischen Balance
Regelstrecke mit globalem I-Verhalten:[5]
- $ G_{S}(s)={\frac {2}{s\cdot (2\cdot s+1)\cdot (0,5\cdot s+1)}} $
Symmetrischer Dreipunktregler mit der Beschreibungsfunktion: ±Umax = ±2; ±Totzone = ±0,5; Führungsgröße w(t) = 1
Geometrische Eckpunkte: Umax = d; Totzone = c
- $ N(A)={\frac {4\cdot d}{\pi \cdot A}}\cdot {\sqrt {1-c^{2}/A^{2}}} $
Ergebnis:
Die Werte der Ortskurve der negativen invertierten Beschreibungsfunktion $ {\frac {-1}{N(A)}} $ werden als $ f(A) $ aus der zugehörigen Gleichung $ N(A) $ des Dreipunktreglers errechnet und auf der reellen Achse Re der Ortskurve des Frequenzgangs eingetragen. Die zwei Äste der Ortskurve beginnen bei $ A=c $, enden bei $ A=\infty $ und kehren die Richtung um bei $ A=1{,}41\;c $. Sie schneiden sich bei $ {\frac {-1}{N(A)}}=-0{,}8 $ mit $ A=1{,}97 $ und $ A=0{,}517 $ mit der Ortskurve des Frequenzgangs bei Realteil von -0,8; $ \omega =1 $.
Die Dauerschwingung mit $ A=0{,}517 $ ist instabil. Die Amplitude $ A=0{,}517 $ liegt im Grenzbereich der Totzone $ c=0{,}5 $, in der noch keine Dauerschwingung möglich ist. Die Beschreibungsfunktion mit der Amplitude $ A=1{,}97 $ ergibt eine stabile Dauerschwingung. Allgemein gilt: die stabile Dauerschwingung stellt sich auf die größere Amplitude ein.
Das mittels numerischer zeitdiskreter Methoden berechnete Diagramm mit dem Zeitverhalten der Systemgrößen stimmt bezüglich der Amplitude und der Frequenz nach dem Einschwingen nach ca. 16 s völlig mit den Ergebnissen der Harmonischen Balance überein.
Stabilität der Grenzschwingungen
Die Ortskurve des Frequenzgangs eines linearen Systems als offener Regelkreis zeigt Dauerschwingungen an, wenn nach dem Nyquist-Verfahren in der komplexen Ebene die Ortskurve den Punkt $ {\mathit {Re}}=-1 $ und $ {\mathit {Im}}=0 $ trifft. Es handelt sich hierbei um keine stabilen Dauerschwingungen, weil bei geringsten Änderungen der Pole von $ G(\mathrm {j} \omega ) $ der kritische Punkt $ {\mathit {Re}}=-1\pm \Delta {\mathit {Re}} $ nicht getroffen wird. Die Folge ist bei einem Wert von $ {\mathit {Re}}=-1+\Delta {\mathit {Re}} $, eine gedämpfte Schwingung tritt auf oder bei einem Wert von $ {\mathit {Re}}=-1-\Delta {\mathit {Re}} $ entsteht eine zunehmend aufklingende Schwingung.
Mit dem Zwei-Ortskurven-Verfahren lassen sich Dauerschwingungen eines nichtlinearen dynamischen zurückgekoppelten Systems ermitteln, wenn in der komplexen Ebene sich die Ortskurven der Beschreibungsfunktion des nichtlinearen Systems und die Ortskurve des Frequenzgangs des linearen Systems treffen. Treffen sich die beiden Ortskurven nicht, handelt es sich um einen schwingungsfreien Regelkreis.
Dabei ist zu berücksichtigen, dass das lineare verzögernde System $ G(\mathrm {j} \omega ) $ von mindestens zweiter Ordnung sein muss, anderenfalls durchläuft die Ortskurve des Frequenzganges nicht den zweiten Quadranten und kann eine auf der realen Achse liegende Ortskurve $ N(A) $ nicht treffen.
Bei einer Dauerschwingung treten Grenzbedingungen für die Beschreibungsfunktion $ N(A) $ auf. Dabei werden die Grenzbedingungen der Schnittpunkte der Ortskurve der Beschreibungsfunktion für drei Fälle betrachtet, bei der die Amplitude $ A $ durch transiente Störungen um einen kleinen Wert $ \Delta A $ erhöht oder vermindert wird und dann jeweils wieder in die Ausgangslage zurückkehrt. Es stellt sich die Frage, was geschieht, wenn eine Dauerschwingung besteht und durch eine kleine vorübergehende Amplitudenänderung positiv oder negativ auf den Gleichgewichtszustand der Dauerschwingung einwirkt. Die Gleichung der harmonischen Balance wird für diese Fälle zu einer Ungleichung.
Folgende Regel gilt für die meisten praktischen Anwendungen und insbesondere für Schnittpunkte mit mehreren ω-Werten für den kleinsten Wert von ω.[6]
|
Der Schnittpunkt der beiden Ortskurven stellt eine stabile Grenzschwingung dar, wenn mit wachsender Amplitude $ A $ der Betrag der Beschreibungsfunktion $ \left|N(A)\right| $ abnimmt. Eine instabile Grenzschwingung ergibt sich, wenn der Betrag von $ \left|N(A)\right| $ mit $ A $ der Beschreibungsfunktion zunimmt. |
Beispiel für einen Regelkreis mit einer Ortskurve eines Dreipunktreglers und einer PT3-Regelstrecke:
Die beiden Zweige der Ortskurve der reellen Beschreibungsfunktion $ N(A) $ liegen negativ invertiert $ {\frac {-1}{N(A)}} $ übereinander auf der reellen Achse.
Es werden folgende drei Fälle unterschieden, bei denen sich die beiden Ortskurven treffen, berühren oder nicht treffen:[7][8]
- Fall 1): Die beiden Ortskurven treffen sich
- Die negativ invertierte Ortskurve der Beschreibungsfunktion $ N(A) $ wird von der Ortskurve des Frequenzgangs $ G(\mathrm {j} \omega ) $ getroffen. Es ergeben sich theoretisch zwei Schnittpunkte und damit zwei Dauerschwingungen gleicher Frequenz mit unterschiedlicher Amplitude. Dies gilt für den Fall, dass auch der kurze Arm der Beschreibungsfunktion $ A=c $ bis $ A={\sqrt {2}}\;c $ (Umkehrpunkt) getroffen wird.
- Nachfolgend wird der Zweig der Beschreibungsfunktion vom Umkehrpunkt $ A={\sqrt {2}}\;c $ im Abstand zur Ordinate mit $ {\frac {-1}{N(A)}}={\frac {-p\;c}{2\;d}} $ mit zunehmender Größe der Amplitude bis $ A=\infty $ betrachtet.
- Wird die Amplitude infolge einer transienten Störung um einen kleinen Betrag $ \Delta A $ vergrößert, liegt der neue Wert $ A_{+} $ links von der Ortskurve des Frequenzgangs $ G(\mathrm {j} \omega ) $ und liegt außerhalb der Ortskurve (nicht umschlungen). Nach dem Nyquist-Kriterium ist der geschlossene Regelkreis stabil. Die Schwingung klingt ab. Nach Ende der Störung wird wieder der Zustand der stabilen Dauerschwingung erreicht.
- Wird die Amplitude infolge einer transienten Störung um einen kleinen Betrag $ \Delta A $ verkleinert, liegt der neue Wert $ A_{-} $ rechts von der Ortskurve des Frequenzgangs $ G(\mathrm {j} \omega ) $. Der neue Wert $ A_{-} $ wird von der Ortskurve $ G(\mathrm {j} \omega ) $ umschlungen und liegt innerhalb des Bereichs der der Ortskurve. Nach dem Nyquist-Kriterium ist der geschlossene Regelkreis instabil. Die Schwingung klingt auf, die Amplitude vergrößert sich auf ihren ursprünglichen Wert. Nach Verschwinden der Störungen ist die Grenzschwingung stabil.
- Fall 2): Die beiden Ortskurven berühren sich am Umkehrpunkt $ A={\sqrt {2}}\;c $ der beiden Äste
- Sind die Schnittpunkte nur Berührungspunkte, dann wird die Grenzschwingung als semistabil bezeichnet.
- Wird die Amplitude infolge einer transienten Störung um einen kleinen Betrag vergrößert, liegt der neue Wert $ A_{+} $ links von der Ortskurve des Frequenzgangs und außerhalb der Ortskurve (nicht umschlungen). Nach dem Nyquist-Kriterium ist der geschlossene Regelkreis stabil. Die Schwingung klingt ab. Nach Ende der Störung wird wieder der Zustand der stabilen Dauerschwingung erreicht.
- Wird die Amplitude infolge einer transienten Störung um einen kleinen Betrag $ \Delta A $ verkleinert, liegt der neue Wert $ A_{-} $ rechts von der Ortskurve des Frequenzgangs $ G(\mathrm {j} \omega ) $ und wird von der Ortskurve $ G(s) $ umschlungen. Die semistabile Grenzschwingung klingt auf. Das Regelsystem ist instabil.
- Fall 3): Die beiden Ortskurven treffen sich nicht und berühren sich nicht
- Der geschlossene Regelkreis ist stabil. Es treten keine Dauerschwingungen auf.
Vermeidung von Dauerschwingungen
Nichtlineare dynamische Systeme können z. B. bei einem Einsatz eines einfachen Zweipunktreglers gewollt stabile Dauerschwingungen hervorrufen. Die Lage der Ortskurve der Beschreibungsfunktion $ {\frac {-1}{N(A)}} $ liegt auf der realen Achse der Ortskurve des Frequenzgangs am Punkt $ {\mathit {Re}}=0 $ und startet bei $ A=0 $ und endet bei $ A=\infty $. Deshalb besteht keine Möglichkeit, mit dem Zweipunktregler Dauerschwingungen zu vermeiden.
Anmerkung: Ein Zweipunktregler schwingt bereits in Verbindung mit einem linearen Verzögerungsglied erster Ordnung, obwohl die beiden Ortskurven sich nicht treffen können. Die Harmonische Balance ist für diesen Fall nicht gültig, weil die Voraussetzung der harmonischen Schwingungen (sägezahnähnliche Schwingung) an $ y(t) $ nicht gegeben sind. Die gilt auch noch für ein Verzögerungsglied zweiter Ordnung (PT2-Glied).
Mit dem Einsatz anderer statischer nichtlinearer Systeme wie z. B. durch den Dreipunktregler lassen sich schwingungsfreie Regelkreise mit asymptotischem Verhalten realisieren. Voraussetzung ist eine Regelstrecke mit globalem I-Verhalten.
Es stellt sich die Frage, welche Maßnahmen mit Hilfe des Zwei-Ortskurven-Verfahrens realisierbar sind.[9]
Folgende Maßnahmen sind gegeben, damit die Gleichung der Harmonischen Balance zu einer Ungleichung wird, bei der sich die beiden Ortskurven nicht treffen können.
Die Ungleichung der Harmonischen Balance könnte lauten:
- $ \left|{\frac {1}{G(\mathrm {j} \omega )}}\right|>\left|N(A)\right|\quad {\text{oder}}\quad 1>\left|N(A)\cdot G(\mathrm {j} \omega )\right| $.
- Reduzierung der Verstärkung des linearen Systems $ G(\mathrm {j} \omega ) $
- Als einfachste Methode könnte die Ortskurve des Frequenzgangs durch Ändern des linearen Systems so gestaltet werden (z. B. Reduzierung der Verstärkung), dass sie die Ortskurve der Beschreibungsfunktion nicht schneidet. Damit würden die dynamischen Eigenschaften des Regelkreises verschlechtert werden.
- Vergrößerung des Abstandes der Ortskurve der Beschreibungsfunktion von der Ordinate bei $ {\mathit {Re}}=0 $.
- Die Ortskurve der Beschreibungsfunktion könnte geändert werden, in dem der Abstand des Umkehrpunktes zur Ordinate der zwei Arme der Beschreibungsfunktion $ {\frac {-\pi \cdot c}{2\cdot d}} $ vergrößert wird. Möglich ist die Verkleinerung der Amplitude $ d $ oder die Vergrößerung der Totzone $ c $.
- Aus regelungstechnischen Gründen in Bezug auf die Genauigkeit der Regelgröße $ y(t) $ muss die Totzone möglichst klein sein, denn auf Regelabweichungen innerhalb der Totzone reagiert der Regler nicht. Die Verkleinerung der Amplitude $ d $ (= Regler-Ausgangsgröße $ \pm U_{\mathrm {max} } $) fordert eine Verkleinerung der Führungsgröße $ w(t) $. Deshalb führt diese Betrachtungsweise zu keinem nennenswerten Ergebnis.
- Teil-Kompensation der Verzögerungsglieder des linearen Systems $ G(\mathrm {j} \omega ) $
- Änderung (Teil-Kompensation) der linearen Regelstrecke durch Einsatz eines realen PD1-Gliedes. Diese Methode der Verbesserung der Systemgeschwindigkeit durch Kompensation träger PT1-Glieder durch reale PD1-Glieder ist auch in der linearen Regelungstechnik üblich. Sie führt auch bei nichtlinearen Regelkreisen zu einem akzeptablen Ergebnis.
Kompensation träger PT1-Glieder durch PD1-Glieder
Durch Austausch träger Verzögerungsglieder des linearen dynamischen Systems erhält das System ein schnelleres Zeitverhalten.
- Beispiel lineare Regelstrecke:
- $ G_{S}(s)={\frac {K}{s\cdot (T_{1}\cdot s+1)\cdot (T_{2}\cdot s+1)}} $
- Lineares reales PD1-Glied (Kompensierglied):
- $ G_{KOMP}(s)={\frac {T_{1}\cdot s+1}{T_{N}\cdot s+1}} $
- Die Zeitkonstante $ T_{1} $ der Strecke soll größer als $ T_{2} $ der Strecke sein. Das PD-Glied mit Zeitkonstante $ T_{1} $ des Reglers soll das Verzögerungsglied mit der Zeitkonstante $ T_{1} $ kompensieren. Die Zeitkonstante $ T_{N} $ muss kleiner $ T_{1} $ sein. Damit ergibt sich die neue Übertragungsfunktion des linearen Regelstrecke in Frequenzgang-Darstellung zu:
- $ G_{S1}(\mathrm {j} \omega )={\frac {K}{\mathrm {j} \omega \cdot (T_{N}\cdot \mathrm {j} \omega +1)\cdot (T_{2}\cdot \mathrm {j} \omega +1)}} $.
- Mit dieser Maßnahme schmiegt sich der Verlauf des Frequenzgangs $ G(\mathrm {j} \omega ) $ näher an die Ordinate beim Durchtreten vom 3. in den 2. Quadranten an. Sind die Parameter der Beschreibungsfunktion so gewählt, dass die beiden Ortskurven sich nicht berühren, ist der Regelkreis asymptotisch stabil. Die Minimierung der Totzone und damit die Optimierung des schwingungsfreien Regelkreises mit einem Dreipunktregler lässt sich nur mit der numerischen Simulation bestimmen.
Beispiel eines schwingungsfreien Regelkreises mit einem Dreipunktregler
Für einen schwingungsfreien Regelkreis mit einem Dreipunktregler wird vorausgesetzt, dass das lineare dynamische System, die Regelstrecke, ein globales I-Verhalten zeigt. Typisch für solche Regelstrecken sind Stellantriebe, die durch den Dreipunktregler auf die Bewegungen Vorlauf, Rücklauf oder Ruhezustand gebracht werden. Der Stillstand entspricht der Soll-Positionierung.
Werden die Parameter des Berechnungsbeispiels des mit Dauerschwingungen behafteten Regelkreises mit dem Dreipunktregler wie folgt modifiziert, entsteht wie in der Grafik dargestellt ein schwingungsfreier Regelkreis.
- Die beiden Verzögerungen der PT1-Glieder werden durch PD1-Glieder um den Faktor 10 reduziert,
- $ G_{0}(\mathrm {j} \omega )={\frac {2}{\mathrm {j} \omega \cdot (0,1\cdot \mathrm {j} \omega +1)\cdot (0,05\cdot \mathrm {j} \omega +1)}} $
- Die bezogene Größe (1 = 100 %) der Rechteck-Schwingamplitude $ \pm U_{\mathrm {max} } $ wird auf $ \pm 1{,}2 $ gesetzt,
- Die bezogene Größe der Totzone wird auf $ \pm c=\pm 0{,}1 $ gesetzt,
- die maximale bezogene Führungsgröße $ w(t)=1 $ gesetzt.
Die Größe der Totzone bestimmt, bei welcher Regelabweichung der Regler ansprechen soll. In diesem Fall richtet sich das Zeitverhalten (Integrationskonstante $ T_{N} $) der auszulegenden Regelstrecke nach der Totzone. Nur ein langsamer Stellantrieb erlaubt für einen schwingungsfreien Betrieb eine kleine Totzone und damit eine genaue Positionierung. Je kleiner die Totzone, umso häufiger und kürzer sind die Rechteckschwingungen $ u(t) $ während des Einschwingvorgangs der Regelgröße $ y(t) $.
Fazit zur Anwendung der Harmonischen Balance
- Die Harmonische Balance zeigt interessante Aspekte des Zustandekommens von Dauerschwingungen in nichtlinearen Regelkreisen und auch Möglichkeiten der Verhinderung von Dauerschwingungen.
- Es gibt kein Berechnungsverfahren der Analyse des Systemverhaltens von nichtlinearen Regelkreisen mit Totzeit- und Hysterese-Elementen, das annähernd so leistungsfähig und gleichzeitig so einfach ist, wie die numerische rekursive Berechnung eines nichtlinearen Systems nach dem Euler-Streckenzug-Verfahren mit der diskreten Zeit $ \Delta t $ und der Berechnungsfolge $ k=(0,1,2,3,\ldots k_{\mathrm {max} }) $.
- Ob die statische Nichtlinearität mit logischen Programmbefehlen und die Linearfaktoren der linearen Teilsysteme mit Differenzengleichungen berechnet werden oder die kommerziellen numerischen Rechenprogramme wie Matlab oder Simulink zur Anwendung kommen, die Erkenntnisse aus der Harmonischen Balance können im Zeitbereich unmittelbar simuliert und bestätigt werden.
Literatur
- Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. 12. Auflage. Europa-Lehrmittel, Haan-Gruiten 2021, ISBN 978-3-8085-5870-6.
- Gerd Schulz: Regelungstechnik 1: Lineare und Nichtlineare Regelung, Rechnergestützter Reglerentwurf. 3. Auflage. Oldenbourg, 2007, ISBN 3-486-58317-4.
- Otto Föllinger: Nichtlineare Regelungen II: Mit Harmonische Balance, Popow- und Kreiskriterium, Hyperstabilität, Synthese im Zustandsraum. 8. Auflage. Oldenbourg, München/ Wien 1993, ISBN 3-486-22503-0.
- Heinz Unbehauen: Regelungstechnik II: Mit Zustandsregelungen, digitale und nichtlineare Regelsysteme. 9. Auflage. Vieweg + Teubner, Wiesbaden 2007, ISBN 978-3-528-83348-0.
Einzelnachweise
- ↑ Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik. Kapitel: Harmonische Linearisierung mit der Beschreibungsfunktion
- ↑ Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik. Kapitel: Nichtlineare Regelungen, Tabelle: Nichtlineare statische Elemente.
- ↑ Jürgen Adamy: Nichtlineare Systeme und Regelungen. 2018, S. 68, doi:10.1007/978-3-662-55685-6 (springer.com [abgerufen am 21. Juni 2020]).
- ↑ Otto Föllinger: Nichtlineare Regelungen II, Harmonische Balance. Kapitel: Lösung der Gleichung der Harmonischen Balance
- ↑ Gerd Schulz: Regelungstechnik 1. Kapitel: Nichtlineare Regler, Praxisbeispiel ist identisch mit Fachbuch!
- ↑ Heinz Unbehauen: Regelungstechnik II. Kapitel: Nichtlineare Regelsysteme, Unterkapitel: Stabilitätsuntersuchung mittels der Beschreibungsfunktion.
- ↑ Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik. Kapitel: Nichtlineare Regelungen, Unterkapitel: Stabilität von Grenzschwingungen.
- ↑ Otto Föllinger: Nichtlineare Regelungen II. Kapitel: Nichtlineare Regelungen, Unterkapitel: Stabilitätsverhalten von Dauerschwingungen.
- ↑ Otto Föllinger: Nichtlineare Regelungen II, Harmonische Balance. Kapitel: Stabilisierung nichtlinearer Regelungen