Inexzyklus
Der Inexzyklus ist ein Finsterniszyklus mit der Periodendauer (die Inexperiode) von etwa 29 Jahren weniger 20 Tage.
Jeder einzelne Inexzyklus enthält theoretisch etwa 809 Sonnen- oder Mondfinsternisse und ist theoretisch etwa 23.410 Jahre lang.[1] Der Niederländer George van den Bergh hat diesen schon vorher erkannten Zyklus wiederentdeckt und ihm den Namen Inex-Zyklus gegeben.
Van den Bergh schuf auch das von ihm so genannte Saros-Inex-Panorama als einen Versuch, alle erdenklichen Finsterniszyklen einfacher zu erkennen als mit einem Finsternis-Canon.[2]
Findung der Inexperiode
Kettenbruch-Rechnung
Die Zahl der in einem Zyklus enthaltenen Finsternisse ist umso größer, je genauer die aus synodischen Monaten bestehende Finsternisperiode ein ganzes Vielfaches von halben drakonitischen Monaten ist. Unter den mit Hilfe von Kettenbruch-Rechnung gefundenen Zahlenpaaren ist das Paar aus 358 synodischen Monaten und 777 halben drakonitischen Monaten (388,5 drakonitische Monate) die Inexperiode.
Van den Berghs Methode
Van den Bergh waren die kurzen Texte in älteren Schriften über den vor ihm namenlosen Zyklus nicht bekannt.[3] Er wendete auch nicht eine relativ einfache Kettenbruch-Rechnung an, sondern fand die Inexperiode durch aufwändige Auswertung des Canon der Finsternisse von Theodor Oppolzer.[4]
Van den Bergh suchte aus dem Canon diejenigen Sonnenfinsternisse heraus, die das mit ±11° angenommene Finsternis-Limit am knappsten unter- oder überbieten. Diese Finsternisse folgen sich in etwa 29 Jahren weniger 20 Tagen, der Inexperiode. Er stellte dabei auch fest, dass sich deren Knotendistanzen um etwa 0,0411° unterscheiden, der Knotendistanz-Änderung in einem Inexzyklus.[5]
Aus dem Eintreten (go IN) dieser gefundenen Finsternisse in die zwischen den Finsternis-Limiten befindliche Zone für zentrale Finsternisse und aus dem Austreten (go EX) bildete van den Bergh den Namen INEX.
Die gefundenen Finsternisse betrachtete van den Bergh nicht als Bestandteil irgendeiner Zyklusreihe (was prinzipiell möglich ist), sondern als je einem Saroszyklus zugehörig. Dieses Vorgehen führte unmittelbar zu seinem Saros-Inex-Panorama.
Saros-Inex-Panorama
Van den Bergh wollte mit seinem Saros-Inex-Panorama den Zank zwischen den Advokaten des Saros- und denjenigen des Inexzyklus beenden helfen.[6]
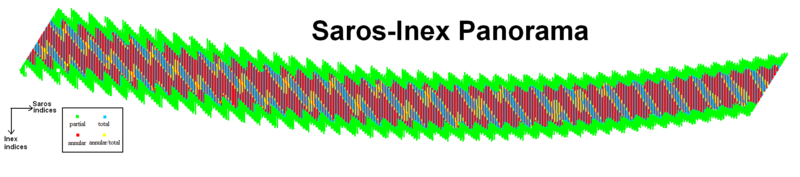
|
In das Panorama ist der Canon der Finsternisse von Oppolzer übertragen. Es ist eine oben und unten “ausgefranste” Tabelle, deren Spalten je alle Finsternisse eines Saroszyklus enthalten; die Zeilen enthalten je alle Finsternisse eines Inexzyklus. Oppolzers Canon war achtmal zu kurz, um die Zeilen auf etwa 800 Finsternisse, die Länge eines Inexzyklus, auszudehnen. Auch mit Hilfe moderner Finsterniskataloge ist das bei weitem noch nicht möglich.[7]
Die Nummern der Spalten haben sich als Nummern der einzelnen Saroszyklen eingebürgert.
Eigenschaften
Da die Zahl der halben drakonitischen Monate ungerade ist (777), finden die Finsternisse anders als bei einem Saroszyklus alternierend in der Nähe des aufsteigenden bzw. des absteigenden Mondknotens statt. Ein Zyklus besteht aus zwei ineinander verschachtelten Finsternisreihen, von denen die eine von Süd nach Nord, die andere von Nord nach Süd verläuft.
Die Knotendistanz-Änderung ist positiv (+0,0411°). Die ersten der in der Nähe des aufsteigenden Knotens stattfindenden Finsternisse finden in der Antarktis statt, die letzten in der Arktis, die Finsternisse beim absteigenden Knoten wandern umgekehrt.
Die etwa 550 in der Mitte der Zyklusdauer stattfindenden Sonnenfinsternisse sind in unregelmäßiger Folge total oder ringförmig-total, weil der anomalistische Monat, anders als beim Saroszyklus, nicht in das Inex-Muster passt (die Entfernung Erde-Mond schwankt während eines Inexzyklus).
Bedeutung
Der Inexzyklus ist wie jeder andere Zyklus ein theoretisches Ergebnis aus einer Kettenbruch-Rechnung. Mit durchschnittlichen Werten für den siderischen und den drakonitischen Monat führt diese zur Inexperiode und zur Knotendistanz-Änderung innerhalb des Inexzyklus. Letztere variiert aber in Realität erheblich gegen den errechneten Mittelwert von 0,0411°. Sie verkleinert sich in 3000 Jahren von 0,0722° auf 0,0294°.[8] Die Veränderung ist mehr als 100 % des errechneten Mittelwertes. Diese Unverhältnismäßigkeit in relativ kurzer Zeit und die sehr große prognostizierte Zyklusdauer sprechen nicht für einen bedeutenden Finsterniszyklus, wie aus den theoretischen Mittelwerten angenommen werden könnte.
Der Inexzyklus hat nur indirekt praktische Bedeutung bekommen, weil van den Bergh im Saros-Inex-Panorama die auch heute noch verwendete Nummerierung der einzelnen Saroszyklen einführte.
Anmerkungen und Einzelnachweise
- ↑ durchschnittliche Werte, siehe Finsterniszyklen
- ↑ George van den Bergh: Periodicity and variation of solar and lunar eclipses, Tjeenk Willink, Haarlem 1955, Seite 32, oben
- ↑ George van den Bergh: Periodicity and variation of solar and lunar eclipses, Tjeenk Willink, Haarlem 1955, Seite 19
- ↑ Theodor Oppolzer: Canon der Finsternisse, Denkschriften der Kaiserlichen Akademie der Wissenschaften mathematisch naturwissenschaftlicher Classe, L II.Bd., Wien 1887
- ↑ George van den Bergh: Periodicity and variation of solar and lunar eclipses, Tjeenk Willink, Haarlem 1955, Seite 15–17
- ↑ George van den Bergh: Periodicity and variation of solar and lunar eclipses, Tjeenk Willink, Haarlem 1955, Seite 33, unten
- ↑ Zum Beispiel ist der Five Millennium Canon of Solar Eclipses: −1999 to +3000 dafür noch fünfmal zu kurz (online)
- ↑ George van den Bergh: Periodicity and variation of solar and lunar eclipses, Tjeenk Willink, Haarlem 1955, Seite 35
Literatur
- George van den Bergh: Periodicity and variation of solar and lunar eclipses, Tjeenk Willink, Haarlem 1955
- Theodor Oppolzer: Canon der Finsternisse, Denkschriften der Kaiserlichen Akademie der Wissenschaften mathematisch naturwissenschaftlicher Classe, L II.Bd., Wien 1887